题目内容
解答题
已知tanα＝3tanβ，其中α、β为锐角，求u＝α＝β的最大值．
答案：
解析：
解析：
|
解：∵α、β为锐角，且tanα＝3tanβ，∴α＞β． ∴0＜α－β＜ 又tanβ＞0，且tanu＝tan(α－β)＝ ＝ 当且仅当 又∵正切函数在(0， ∴u＝α－β≤ 故u的最大值为 |
．
＝
＝
≤
＝
．
＝3tanβ，即tanβ＝
，亦即β＝
时取等号．
)内单调递增，
．
，此时α＝
，β＝
．
练习册系列答案
轻松暑假总复习系列答案
相关题目
．
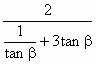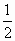，且
π＜α＜
π，
)的值．
)＝
＋
．