题目内容
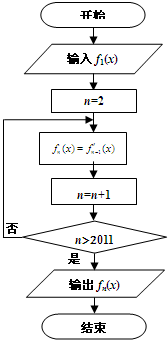 在如图所示的程序框图中,当n∈N*(n>1)时,函数fn(x)表示函数fn-1(x)的导函数,若输入函数f1(x)=sinx+cosx,则输出的函数fn(x)可化为( )
在如图所示的程序框图中,当n∈N*(n>1)时,函数fn(x)表示函数fn-1(x)的导函数,若输入函数f1(x)=sinx+cosx,则输出的函数fn(x)可化为( )A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
分析:先根据流程图弄清概括程序的功能,然后计算分别f1(x),f2(x)、f3(x)、f4(x)、f5(x),得到周期,从而求出f2009(x)的解析式.
解答:解:由框图可知n=2011时输出结果,
由于f1(x)=sinx+cosx,
f2(x)=-sinx+cosx,
f3(x)=-sinx-cosx,
f4(x)=sinx-cosx,
f5(x)=sinx+cosx,
所以f2009(x)=f4×501+5(x)=sinx+cosx=
sin(x+
).
故选C.
由于f1(x)=sinx+cosx,
f2(x)=-sinx+cosx,
f3(x)=-sinx-cosx,
f4(x)=sinx-cosx,
f5(x)=sinx+cosx,
所以f2009(x)=f4×501+5(x)=sinx+cosx=
| 2 |
| π |
| 4 |
故选C.
点评:本题主要考查了直到型循环结构,以及从识别流程图,整体把握,概括程序的功能,同时考查周期性,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

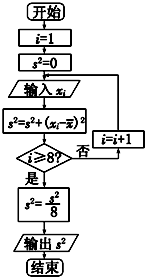 一组数据xi(1≤i≤8)从小到大茎叶图如图:4|0 1 3 3 4 6 7 8,在如图所示的程序框图中
一组数据xi(1≤i≤8)从小到大茎叶图如图:4|0 1 3 3 4 6 7 8,在如图所示的程序框图中 (2012•青州市模拟)在一次演讲比赛中,10位评委对一名选手打分的茎叶图如图所示,若去掉一个最高分和一个最低分,得到一组数据xi(1≤i≤8),在如图所示的程序框图中,
(2012•青州市模拟)在一次演讲比赛中,10位评委对一名选手打分的茎叶图如图所示,若去掉一个最高分和一个最低分,得到一组数据xi(1≤i≤8),在如图所示的程序框图中,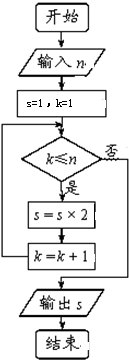 在如图所示的程序框图中输入3,结果会输出
在如图所示的程序框图中输入3,结果会输出