Question

若PA⊥平面ABC,AC⊥BC,PA=AC=1,BC=,求二面角A—PB—C的余弦值.

Answer 1

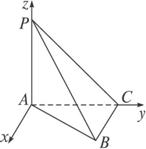
解：如图所示建立空间直角坐标系,则A(0,0,0),B(,1,0),C(0,1,0),P(0,0,1),=(0,0,1), =(,1,0),=(,0,0),=(0,-1,1),设平面PAB的法向量为m=(x,y,z),则

令x=1,则m=(1,-，0).

设平面PBC的法向量为n=（x′,y′,z′），则

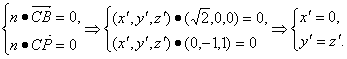
令y′=-1,则n=(0,-1,-1),

∴cos〈m,n〉=.

∴二面角A—PB—C的余弦值为.