题目内容
设函数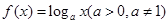 ,已知数列
,已知数列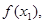
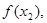
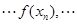 是公差为2的等差数列,且
是公差为2的等差数列,且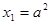 .
.
(Ⅰ)求数列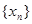 的通项公式;
的通项公式;
(Ⅱ)当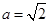 时,求数列
时,求数列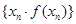 的前
的前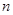 项和
项和 .
.
【答案】
(Ⅰ)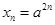 .(Ⅱ)
.(Ⅱ)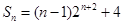 .
.
【解析】
试题分析:(Ⅰ)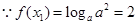 ,且
,且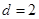 ,
,
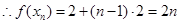 ,即
,即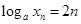 ,
,
所以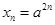 . 6分
. 6分
(Ⅱ)当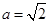 时,
时,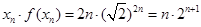 ,
,
则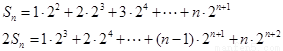 ,
8分
,
8分
两式相减得
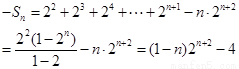 , 11分
, 11分
所以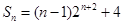 .
12分
.
12分
考点:本题主要考查等比数列的的基础知识,对数函数的性质,“错位相消法”求和。
点评:中档题,本题综合考查、等比数列的基础知识,对数函数的性质,本解答从确定通项公式入手,明确了所研究数列的特征。“分组求和法”、“错位相消法”、“裂项相消法”是高考常常考到数列求和方法。

练习册系列答案
相关题目
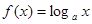 (
( ),已知数列
),已知数列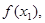
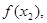
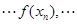 是公差为2的等差数列,且
是公差为2的等差数列,且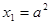 .
.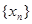 的通项公式;
的通项公式;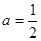 时,求证:
时,求证: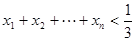 .
.