题目内容
(理)袋中有大小相同的红球和白球若干个,其中红、白球个数的比为4:3.假设从袋中任取2个球,取到的都是红球的概率为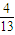 .
.(1)试问:袋中的红、白球各有多少个?
(2)现从袋中逐次取球,每次从袋中任取1个球,若取到白球,则停止取球,若取到红球,则继续下一次取球.试求:取球不超过3次便停止的概率.
【答案】分析:(1)由于已知红、白球个数的比为4:3故可设袋中有红球4k个,白球3k个,再由题设中假设从袋中任取2个球,取到的都是红球的概率为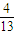 建立方程求出红、白球各有多少个.
建立方程求出红、白球各有多少个.
(2)由题意,记A为“取球不超过3次便停止”;Bi(i=1,2,3)为“第i次取到红球”,则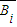 为“第i次取到白球”,由相互独立事件的概率乘法公式求出概率即可
为“第i次取到白球”,由相互独立事件的概率乘法公式求出概率即可
解答:解:(1)设袋中有红球4k个,白球3k个,由题设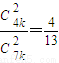 ,解得k=2,…(4分)
,解得k=2,…(4分)
因此,袋中有红球8个,白球6个. …(6分)
(2)记A为“取球不超过3次便停止”;Bi(i=1,2,3)为“第i次取到红球”,则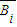 为“第i次取到白球”.
为“第i次取到白球”.
由题设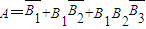 ,且
,且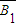 、
、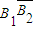 、
、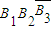 为互不相容事件,B1、
为互不相容事件,B1、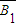 、B2、
、B2、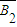 、
、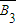 为互相独立事件,…(10分)
为互相独立事件,…(10分)
故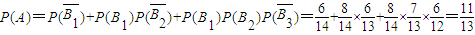 .…(14分)
.…(14分)
点评:本题考查相互独立事件的概率乘法公式与等可能事件的概率求法,第二小题中理解事件“取球不超过3次便停止”是解题的关键,第一题中由两种颜色的球的个数比设出它们的个数是关键,第二小题的求解是本题的难点,
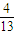 建立方程求出红、白球各有多少个.
建立方程求出红、白球各有多少个.(2)由题意,记A为“取球不超过3次便停止”;Bi(i=1,2,3)为“第i次取到红球”,则
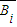 为“第i次取到白球”,由相互独立事件的概率乘法公式求出概率即可
为“第i次取到白球”,由相互独立事件的概率乘法公式求出概率即可解答:解:(1)设袋中有红球4k个,白球3k个,由题设
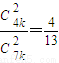 ,解得k=2,…(4分)
,解得k=2,…(4分)因此,袋中有红球8个,白球6个. …(6分)
(2)记A为“取球不超过3次便停止”;Bi(i=1,2,3)为“第i次取到红球”,则
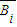 为“第i次取到白球”.
为“第i次取到白球”.由题设
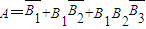 ,且
,且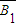 、
、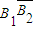 、
、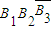 为互不相容事件,B1、
为互不相容事件,B1、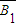 、B2、
、B2、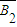 、
、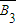 为互相独立事件,…(10分)
为互相独立事件,…(10分)故
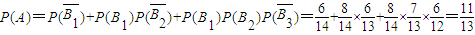 .…(14分)
.…(14分)点评:本题考查相互独立事件的概率乘法公式与等可能事件的概率求法,第二小题中理解事件“取球不超过3次便停止”是解题的关键,第一题中由两种颜色的球的个数比设出它们的个数是关键,第二小题的求解是本题的难点,

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目