题目内容
判断下列各函数的奇偶性:
(1)f(x)=(x-2)![]() ;
;
(2)f(x)=![]() ;
;
(3)f(x)=
(1)f(x)为非奇非偶函数(2)f(x)为偶函数(3)f(x)是偶函数
解析:
(1)由![]() ≥0,得定义域为[-2,2),关于原点不对称,故f(x)为非奇非偶函数.
≥0,得定义域为[-2,2),关于原点不对称,故f(x)为非奇非偶函数.
(2)由![]() 得定义域为(-1,0)∪(0,1).
得定义域为(-1,0)∪(0,1).
这时f(x)=![]() .
.
∵f(-x)=-![]() ∴f(x)为偶函数.
∴f(x)为偶函数.
(3)x<-1时,f(x)=x+2,-x>1,
∴f(-x)=-(-x)+2=x+2=f(x).
x>1时,f(x)=-x+2,
-x<-1,f(-x)=x+2=f(x).
-1≤x≤1时,f(x)=0,-1≤-x≤1,
f(-x)=0=f(x).
∴对定义域内的每个x都有f(-x)=f(x).因此f(x)是偶函数.

练习册系列答案
 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案 互动课堂系列答案
互动课堂系列答案
相关题目
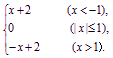
 ;
; ;
;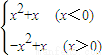 .
.