题目内容
下面有五个命题:
①函数 的最小正周期是
的最小正周期是
②终边在y轴上的角的集合是{ }
}
③在同一坐标系中,函数 的图象和函数y=x的图象有三个公共点
的图象和函数y=x的图象有三个公共点
④把函数 的图象向右平移
的图象向右平移 得到
得到 的图象
的图象
⑤函数 上是减函数
上是减函数
其中,真命题的编号是 (写出所有真命题的编号)
①④
解析试题分析:∵函数y=sin4x-cos4x=-cos2x,最小正周期是T=π,故①正确;
终边在y轴上的角的集合是{a|a=kπ+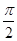 ,k∈Z};故②不正确;
,k∈Z};故②不正确;
由 得sinx=x,令g(x)=x-sinx,g′(x)=1-cosx≥0,
得sinx=x,令g(x)=x-sinx,g′(x)=1-cosx≥0,
故g(x)=x-sinx在R上单调递增,当x=0时g′(0)=0,
∴g(x)min=g(0)=0,即在同一坐标系中,函数y=sinx的图象和函数y=x的图象有一个公共点,故③不正确;
函数y=3sin(2x+ )的图象向右平移
)的图象向右平移 得到y=3sin[2(x-
得到y=3sin[2(x- )+
)+ ]=3sin2x,故④正确;
]=3sin2x,故④正确;
∵y=sin(x-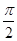 )=-cosx在(0,π)上是增函数,故⑤不正确.故答案为①④。
)=-cosx在(0,π)上是增函数,故⑤不正确.故答案为①④。
考点:本题主要考查正弦型函数的图象和性质,倍角公式,诱导公式,应用导数研究函数的单调性。
点评:中档题,本题综合性较强,较全面考查正弦型函数的图象和性质,倍角公式,诱导公式,应用导数研究函数的单调性。其中对命题(3)的研究利用导数,往往难以想到。

练习册系列答案
相关题目
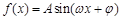
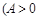 ,
,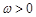 ,
,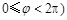 在
在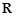 上的部分图象如图所示,则
上的部分图象如图所示,则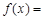 .
. 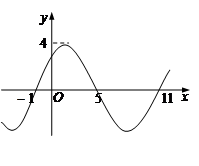
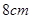 ,面积为
,面积为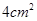 ,则扇形的圆心角的弧度数是 。
,则扇形的圆心角的弧度数是 。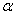 的终边与单位圆的交点坐标为(
的终边与单位圆的交点坐标为(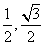 ),则
),则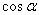 = .
= .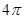 的扇形的圆心角为
的扇形的圆心角为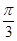 ,则此扇形的面积为 ;
,则此扇形的面积为 ; 在第一象限是增函数;②函数
在第一象限是增函数;②函数 是偶函数; ③函数
是偶函数; ③函数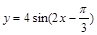 的一个对称中心是(
的一个对称中心是(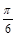 ,0);④函数
,0);④函数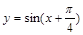 在闭区间
在闭区间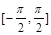 上是增函数; 写出所有正确的命题的题号: 。
上是增函数; 写出所有正确的命题的题号: 。