题目内容
已知函数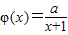 ,a为正常数.
,a为正常数.(Ⅰ)若f(x)=lnx+φ(x),且
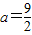 ,求函数f(x)的单调减区间;
,求函数f(x)的单调减区间;(Ⅱ)若g(x)=|lnx|+φ(x),且对任意x1,x2∈(0,2],x1≠x2,都有
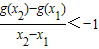 ,求a的取值范围.
,求a的取值范围.
【答案】分析:(Ⅰ)求导函数,令其小于0,结合函数的定义域,可求函数的单调减区间;
(Ⅱ)由已知,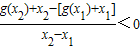 ,构造h(x)=g(x)+x,利用导数研究其单调性,及最值进行求解.
,构造h(x)=g(x)+x,利用导数研究其单调性,及最值进行求解.
解答:解:(Ⅰ)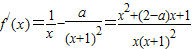 ,∵
,∵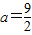 ,令f′(x)<0,
,令f′(x)<0,
得 ,故函数f(x)的单调减区间为
,故函数f(x)的单调减区间为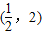 . …(5分)
. …(5分)
(Ⅱ)∵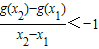 ,∴
,∴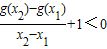 ,
,
∴ ,
,
设h(x)=g(x)+x,依题意,h(x)在(0,2]上是减函数,当1≤x≤2时,h(x)=lnx+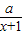 +x,
+x,
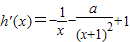 ,令h′(x)≤0,得a
,令h′(x)≤0,得a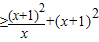 ═
═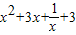 对x∈[1,2]恒成立
对x∈[1,2]恒成立
设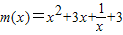 ,则
,则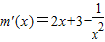 ,
,
∵1≤x≤2,∴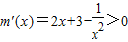 ,
,
∴m(x)在[1,2]上是增函数,则当x=2时,m(x)有最大值为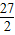 ,∴
,∴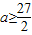 .
.
当0<x<1时, ,
,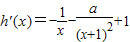 ,
,
令h'(x)≤0,得: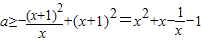 ,
,
设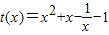 ,则
,则 ,∴t(x)在(0,1)上是增函数,
,∴t(x)在(0,1)上是增函数,
∴t(x)<t(1)=0,∴a≥0,综上所述,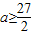 . …(16分)
. …(16分)
点评:本题考查函数单调性与导数的关系及应用,考查转化、计算能力.
(Ⅱ)由已知,
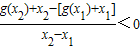 ,构造h(x)=g(x)+x,利用导数研究其单调性,及最值进行求解.
,构造h(x)=g(x)+x,利用导数研究其单调性,及最值进行求解.解答:解:(Ⅰ)
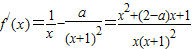 ,∵
,∵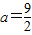 ,令f′(x)<0,
,令f′(x)<0,得
 ,故函数f(x)的单调减区间为
,故函数f(x)的单调减区间为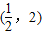 . …(5分)
. …(5分)(Ⅱ)∵
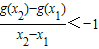 ,∴
,∴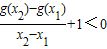 ,
,∴
 ,
,设h(x)=g(x)+x,依题意,h(x)在(0,2]上是减函数,当1≤x≤2时,h(x)=lnx+
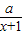 +x,
+x,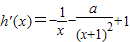 ,令h′(x)≤0,得a
,令h′(x)≤0,得a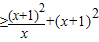 ═
═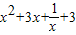 对x∈[1,2]恒成立
对x∈[1,2]恒成立设
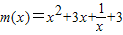 ,则
,则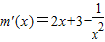 ,
,∵1≤x≤2,∴
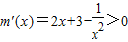 ,
,∴m(x)在[1,2]上是增函数,则当x=2时,m(x)有最大值为
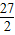 ,∴
,∴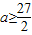 .
.当0<x<1时,
 ,
,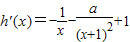 ,
,令h'(x)≤0,得:
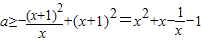 ,
,设
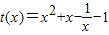 ,则
,则 ,∴t(x)在(0,1)上是增函数,
,∴t(x)在(0,1)上是增函数,∴t(x)<t(1)=0,∴a≥0,综上所述,
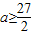 . …(16分)
. …(16分)点评:本题考查函数单调性与导数的关系及应用,考查转化、计算能力.

练习册系列答案
相关题目
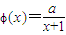 ,a为正常数.
,a为正常数. ,求函数f(x)的单调增区间;
,求函数f(x)的单调增区间;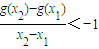 ,求a的取值范围.
,求a的取值范围.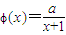 ,a为正常数.
,a为正常数. ,求函数f(x)的单调增区间;
,求函数f(x)的单调增区间;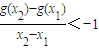 ,求a的取值范围.
,求a的取值范围.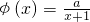 ,a为正常数.
,a为正常数.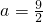 ,求函数f(x)的单调增区间;
,求函数f(x)的单调增区间;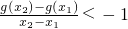 ,求a的取值范围.
,求a的取值范围.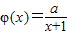 ,a为正常数.
,a为正常数.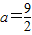 ,求函数f(x)的单调增区间;
,求函数f(x)的单调增区间;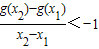 ,求a的取值范围.
,求a的取值范围.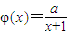 ,a为正常数.
,a为正常数. ,求函数f(x)的单调增区间;
,求函数f(x)的单调增区间; ,求a的取值范围.
,求a的取值范围.