题目内容
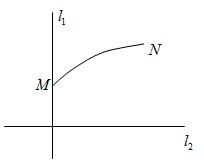 如图,l1、l2是通过某城市开发区中心O的两条南北和东西走向的街道,连接M、N两地之间的铁路线是圆心在l2上的一段圆弧.若点M在点O正北方向,且|MO|=3km,点N到l1、l2的距离分别为4km和5km.
如图,l1、l2是通过某城市开发区中心O的两条南北和东西走向的街道,连接M、N两地之间的铁路线是圆心在l2上的一段圆弧.若点M在点O正北方向,且|MO|=3km,点N到l1、l2的距离分别为4km和5km.(1)建立适当坐标系,求铁路线所在圆弧的方程;
(2)若该城市的某中学拟在点O正东方向选址建分校,考虑环境问题,要求校址到点O的距离大于4km,并且铁路线上任意一点到校址的距离不能少于
| 26 |
分析:(1)建立坐标系,利用圆心在弦的垂直平分线上求圆心坐标,再求半径,进而写出圆的方程.
(2)据条件列出不等式,运用函数单调性解决恒成立问题.
(2)据条件列出不等式,运用函数单调性解决恒成立问题.
解答:解:(1)分别以l2、l1为x轴,y轴建立如图坐标系.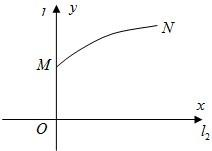
据题意得M(0,3),N(4,5),∴kMN=
=
,
MN中点为(2,4),
∴线段MN的垂直平分线方程为:y-4=-2(x-2)),
故圆心A的坐标为(4,0),
半径r=
=5,(5分)
∴弧
的方程为:(x-4)2+y2=25(0≤x≤4,5≥y≥3).(8分)
(2)设校址选在B(a,0)(a>4),
则
≥
,对0≤x≤4恒成立.
即
≥
,对0≤x≤4恒成立.
整理得:(8-2a)x+a2-17≥0,对0≤x≤4恒成立(﹡).(10分)
令f(x)=(8-2a)x+a2-17.
∵a>4,∴8-2a<0,
∴f(x)在[0,4]上为减函数,(12分)
∴要使(﹡)恒成立,当且仅当
,即
,
解得a≥5,(14分)
即校址选在距O最近5km的地方.(16分)

据题意得M(0,3),N(4,5),∴kMN=
| 5-3 |
| 4-0 |
| 1 |
| 2 |
MN中点为(2,4),
∴线段MN的垂直平分线方程为:y-4=-2(x-2)),
故圆心A的坐标为(4,0),
半径r=
| (4-0)2+(0-3)2 |
∴弧
 |
| MN |
(2)设校址选在B(a,0)(a>4),
则
| (x-a)2+y2 |
| 26 |
即
| (x-a)2+25-(x-4)2 |
| 26 |
整理得:(8-2a)x+a2-17≥0,对0≤x≤4恒成立(﹡).(10分)
令f(x)=(8-2a)x+a2-17.
∵a>4,∴8-2a<0,
∴f(x)在[0,4]上为减函数,(12分)
∴要使(﹡)恒成立,当且仅当
|
|
解得a≥5,(14分)
即校址选在距O最近5km的地方.(16分)
点评:本题主要考查求点的轨迹方程的方法,函数的恒成立问题,利用二次函数在闭区间上的单调性求函数的值域,
属于中档题.
属于中档题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 ,求该校址距点O的最近距离(注:校址视为一个点).
,求该校址距点O的最近距离(注:校址视为一个点).
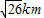 ,求该校址距点O的最近距离(注:校址视为一个点).
,求该校址距点O的最近距离(注:校址视为一个点).
 ,求该校址距点O的最近距离(注:校址视为一个点).
,求该校址距点O的最近距离(注:校址视为一个点).
 ,求该校址距点O的最近距离(注:校址视为一个点).
,求该校址距点O的最近距离(注:校址视为一个点).