题目内容
已知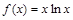 .
.
(1)求函数 在区间
在区间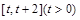 上的最小值;
上的最小值;
(2)对一切实数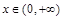 ,
, 恒成立,求实数
恒成立,求实数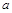 的取值范围;
的取值范围;
(3)证明对一切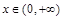 ,
,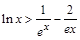 恒成立.
恒成立.
【答案】
(1)
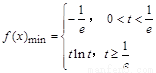
(2)4
(3)证明略
【解析】解:⑴ 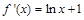 ,当
,当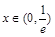 ,
,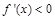 ,
,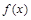 单调递减,
单调递减,
当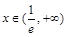 ,
,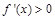 ,
,
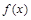 单调递增.
单调递增.
① 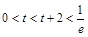 ,t无解;
,t无解;
② 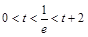 ,即
,即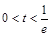 时,
时,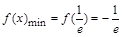 ;
;
③ 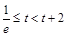 ,即
,即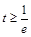 时,
时,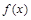 在
在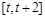 上单调递增,
上单调递增,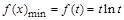 ;
;
所以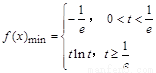 .
.
⑵ 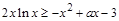 ,则
,则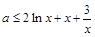 ,设
,设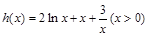 ,
,
则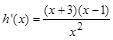 ,
,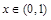 ,
,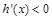 ,
,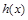 单调递增,
单调递增,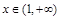 ,
,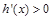 ,
,
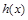 单调递减, 所以
单调递减, 所以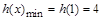 ,
,
因为对一切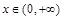 ,
,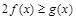 恒成立,
恒成立,
所以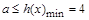 ;
;
⑶ 问题等价于证明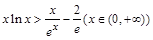 ,
,
由⑴可知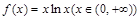 的最小值是
的最小值是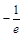 ,当且仅当
,当且仅当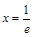 时取到,
时取到,
设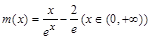 ,则
,则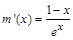 ,易得
,易得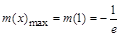 ,
,
当且仅当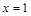 时取到,从而对一切
时取到,从而对一切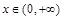 ,都有
,都有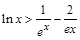 成立.
成立.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
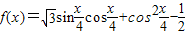 .
.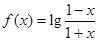 .
.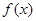 的定义域;
的定义域;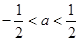 ,试比较
,试比较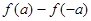 与
与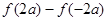 的大小.
的大小.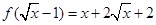 ,
,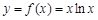 .
.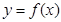 的图像在
的图像在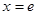 处的切线方程;
处的切线方程;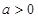 ,求函数
,求函数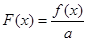 在
在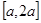 上的最大值;
上的最大值;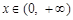 ,都有
,都有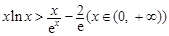 成立。
成立。