题目内容
 高一年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
高一年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:(1)根据下面图表,①②③处的数值分别为
1
1
、0.100
0.100
、40
40
;(2)在所给的坐标系中画出[85,155]的频率分布直方图;
(3)根据题中信息估计总体平均数.
| 分组 | 频数 | 频率 |
| [85,95) | ① | 0.025 |
| [95,105) | 0.050 | |
| [105,115) | 0.200 | |
| [115,125) | 12 | 0.300 |
| [125,135) | 0.275 | |
| [135,145) | 4 | ② |
| [145,155] | 0.050 | |
| 合计 | ③ |
分析:(1)根据频率的求法,频率=
,计算可得答案.
(2)欲画频率分布直方图,清楚显示在各个不同区间内取值,各组频数分布情况,并把各
作为小矩形的高,作出频率分布直方图;
(3)为了根据题中信息估计总体平均数,先利用组中值求样本的平均数,再利用样本的平均数估计总体平均数即可.
| 频数 |
| 数据总和 |
(2)欲画频率分布直方图,清楚显示在各个不同区间内取值,各组频数分布情况,并把各
| 频率 |
| 组数 |
(3)为了根据题中信息估计总体平均数,先利用组中值求样本的平均数,再利用样本的平均数估计总体平均数即可.
解答:解:(1)由第四小组知:总数=
=40,故③=40,②=
=0.1,①=0.025×40=1.
①②③处的数值分别为1,0.100,40.
故答案为:1,0.100,40.
(2)在所给的坐标系中画出[85,155]的频率分布直方图;
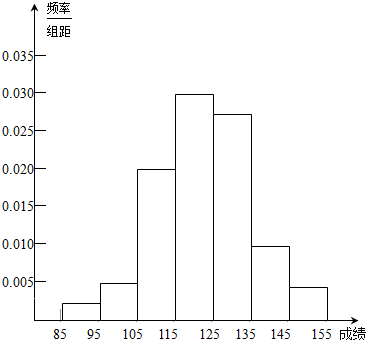
(3)根据题中信息估计总体平均数.
利用组中值得平均数
=90×0.025+100×0.05+110×0.2+120×0.3+130×0.275+140×0.1+150×0.05=122.5
所以估计总体平均数为122.5.
| 12 |
| 0.3 |
| 4 |
| 40 |
①②③处的数值分别为1,0.100,40.
故答案为:1,0.100,40.
(2)在所给的坐标系中画出[85,155]的频率分布直方图;

(3)根据题中信息估计总体平均数.
利用组中值得平均数
. |
| x |
所以估计总体平均数为122.5.
点评:本题考查读频数分布直方图的能力和利用统计图获取信息的能力.利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
高一年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
⑴根据下面图表,①②③处的数值分别为 、 、 ;
⑵在所给的坐标系中画出[85,155]的频率分布直方图;
⑶根据题中信息估计总体平均数.
| 分组 | 频数 | 频率 |
|
| ① | 0.025 |
|
| 0.050 | |
|
| 0.200 | |
|
| 12 | 0.300 |
|
| 0.275 | |
|
| 4 | ② |
| [145,155] | 0.050 | |
| 合计 | ③ |

高一年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
(1)根据上面图表,①②③④处的数值分别为多少?
(2)根据题中信息估计总体平均数是多少?
(3)估计总体落在[129,150]中的概率.
| 分组 | 频数 | 频率 |
| [85,95) | ① | ② |
| [95,105) | 0.050 | |
| [105,115) | 0.200 | |
| [115,125) | 12 | 0.300 |
| [125,135) | 0.275 | |
| [135,145) | 4 | ③ |
| [145,155] | 0.050 | |
| 合计 | ④ |
(2)根据题中信息估计总体平均数是多少?
(3)估计总体落在[129,150]中的概率.
高一年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
(1)根据上面图表,①②③④处的数值分别为多少?
(2)根据题中信息估计总体平均数是多少?
(3)估计总体落在[129,150]中的概率.
| 分组 | 频数 | 频率 |
| [85,95) | ① | ② |
| [95,105) | 0.050 | |
| [105,115) | 0.200 | |
| [115,125) | 12 | 0.300 |
| [125,135) | 0.275 | |
| [135,145) | 4 | ③ |
| [145,155] | 0.050 | |
| 合计 | ④ |
(2)根据题中信息估计总体平均数是多少?
(3)估计总体落在[129,150]中的概率.