题目内容
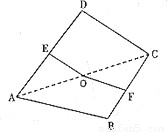
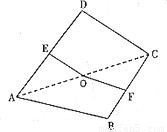
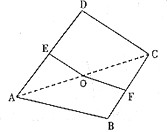 如图,点O是正方形纸片ABCD的中心,点E,F分别为AD,BC的中点,现沿对角线AC把纸片折成直二面角,则纸片折后∠EOF的大小为
如图,点O是正方形纸片ABCD的中心,点E,F分别为AD,BC的中点,现沿对角线AC把纸片折成直二面角,则纸片折后∠EOF的大小为
- A.30°
- B.60°
- C.120°
- D.150°
C
分析:过过F作FG垂直于AC,G在AC上,连接GE,由三余弦定理可得cos∠EOF=cos∠FOG•cos∠GOE,根据正方形的性质及等腰直角三角形的性质,我们易得∠AOF=135°,∠AOE=45°,进而我们可以求出∠EOF的余弦值,进而得到∠EOF的大小.
解答:过F作FG垂直于AC,G在AC上,连接GE;
∵二面角B-AC-D为直二面角,
∴FG⊥平面ACD(直二面角的性质),
∵FO为平面ADC的斜线,OE在平面ADC内,
由三余弦定理得:cos∠EOF=cos∠FOG•cos∠GOE…(1)
∵∠FOG=180°-∠AOF,∠GOE=180°-∠AOE(邻补角定义),代入(1)得:
cos∠EOF=(-cos∠AOF)•(-cos∠AOE),
即cos∠EOF=cos∠AOF*cos∠AOE.
由∠AOF=135°,∠AOE=45°
∴cos∠EOF=cos135°•cos45°=-
则∠EOF=120°
故选C
点评:本题考查的知识点是与二面角有关的立体几何综合题,其中过F作FG垂直于AC,为三余弦定理的使用创造条件,是解答本题的关键.
分析:过过F作FG垂直于AC,G在AC上,连接GE,由三余弦定理可得cos∠EOF=cos∠FOG•cos∠GOE,根据正方形的性质及等腰直角三角形的性质,我们易得∠AOF=135°,∠AOE=45°,进而我们可以求出∠EOF的余弦值,进而得到∠EOF的大小.
解答:过F作FG垂直于AC,G在AC上,连接GE;
∵二面角B-AC-D为直二面角,
∴FG⊥平面ACD(直二面角的性质),
∵FO为平面ADC的斜线,OE在平面ADC内,
由三余弦定理得:cos∠EOF=cos∠FOG•cos∠GOE…(1)
∵∠FOG=180°-∠AOF,∠GOE=180°-∠AOE(邻补角定义),代入(1)得:
cos∠EOF=(-cos∠AOF)•(-cos∠AOE),
即cos∠EOF=cos∠AOF*cos∠AOE.
由∠AOF=135°,∠AOE=45°
∴cos∠EOF=cos135°•cos45°=-

则∠EOF=120°
故选C
点评:本题考查的知识点是与二面角有关的立体几何综合题,其中过F作FG垂直于AC,为三余弦定理的使用创造条件,是解答本题的关键.

练习册系列答案
相关题目
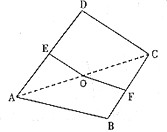 如图,点O是正方形纸片ABCD的中心,点E,F分别为AD,BC的中点,现沿对角线AC把纸片折成直二面角,则纸片折后∠EOF的大小为( )
如图,点O是正方形纸片ABCD的中心,点E,F分别为AD,BC的中点,现沿对角线AC把纸片折成直二面角,则纸片折后∠EOF的大小为( )| A、30° | B、60° | C、120° | D、150° |