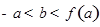题目内容
已知函数![]()
(1)设曲线![]() 在
在![]() 处的切线与直线
处的切线与直线![]() 垂直,求
垂直,求![]() 的值;
的值;
(2)若对任意实数![]() 恒成立,确定实数
恒成立,确定实数![]() 的取值范围;
的取值范围;
(3)当![]() 时,是否存在实数
时,是否存在实数![]() ,使曲线C:
,使曲线C:![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴垂直?若存在,求出
轴垂直?若存在,求出![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
(1)![]() , 因此
, 因此![]() 在
在![]() 处的切线
处的切线![]() 的斜率为
的斜率为![]() ,
,
又直线![]() 的斜率为
的斜率为![]() , ∴(
, ∴(![]() )
)![]() =-1,
=-1,
∴ ![]() =-1.
=-1.
(2)∵当![]() ≥0时,
≥0时,![]()
![]() 恒成立,
恒成立,
∴ 先考虑![]() =0,此时,
=0,此时,![]() ,
,![]() 可为任意实数;
可为任意实数;
又当![]() >0时,
>0时,![]()
![]() 恒成立,
恒成立,
则![]() 恒成立, 设
恒成立, 设![]() =
=![]() ,则
,则![]() =
=![]() ,
,
当![]() ∈(0,1)时,
∈(0,1)时,![]() >0,
>0,![]() 在(0,1)上单调递增,
在(0,1)上单调递增,
当![]() ∈(1,+∞)时,
∈(1,+∞)时,![]() <0,
<0,![]() 在(1,+∞)上单调递减,
在(1,+∞)上单调递减,
故当![]() =1时,
=1时,![]() 取得极大值,
取得极大值,![]() ,
,
∴ 实数![]() 的取值范围为
的取值范围为![]() .
.
(3)依题意,曲线C的方程为![]() ,
,
令![]() =
=![]() ,则
,则![]()
设![]() ,则
,则![]() ,
,
当![]() ,
,![]() ,故
,故![]() 在
在![]() 上的最小值为
上的最小值为![]() ,
,
所以![]() ≥0,又
≥0,又![]() ,∴
,∴![]() >0,
>0,
而若曲线C:![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴垂直,
轴垂直,
则![]() =0,矛盾。
=0,矛盾。
所以,不存在实数![]() ,使曲线C:
,使曲线C:![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴垂直.
轴垂直.

练习册系列答案
相关题目
 .
. 在
在 和
和 处的切线相互平行,求
处的切线相互平行,求 的值;
的值; ,对任意的
,对任意的 ,均存在
,均存在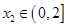 ,使得
,使得 .试求实数
.试求实数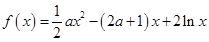 .
.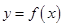 在
在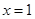 和
和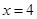 处的切线相互平行,求
处的切线相互平行,求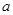 的值;
的值;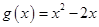 ,对任意的
,对任意的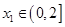 ,均存在
,均存在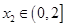 ,使得
,使得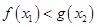 .试求实数
.试求实数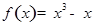 .
.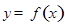 在点
在点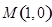 处的切线方程;
处的切线方程;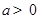 ,如果过点
,如果过点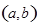 可作曲线
可作曲线