题目内容
实数x，y满足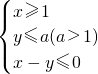
若目标函数z=x+y取得最大值4，则实数a的值为
- A.4
- B.3
- C.2
- D.
C
分析：作出不等式组表示的可行域，将目标函数变形y=-x+z，判断出z表示直线的纵截距，结合图象，求出k的范围
解答：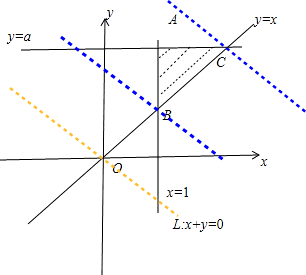
解：作出不等式组表示的平面区域，如图所示
∵y=-x+z，则z表示直线的纵截距
做直线L：x+y=0，然后把直线L向可行域平移，结合图象可知，平移到C（a，a）时，z最大
此时z=2a=4
∴a=2
故选C
点评：解决此类问题的关键是正确画出不等式组表示的可行域，将目标函数赋予几何意义．
分析：作出不等式组表示的可行域，将目标函数变形y=-x+z，判断出z表示直线的纵截距，结合图象，求出k的范围
解答：
解：作出不等式组表示的平面区域，如图所示∵y=-x+z，则z表示直线的纵截距
做直线L：x+y=0，然后把直线L向可行域平移，结合图象可知，平移到C（a，a）时，z最大
此时z=2a=4
∴a=2
故选C
点评：解决此类问题的关键是正确画出不等式组表示的可行域，将目标函数赋予几何意义．
练习册系列答案
阳光课堂同步练习系列答案
相关题目
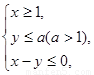若目标函数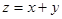
取得最大值4，则实数
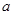的值为( )
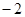B．2 C．1 D．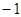
若目标函数z=ax+y（a≠0）取得最小值时的最优解有无数个，则实数a的值为 ．
若目标函数z=ax+y（a≠0）取得最小值时的最优解有无数个，则实数a的值为 ．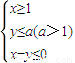
若目标函数z=x+y取得最大值4，则实数a的值为（ ）
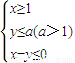若目标函数z=x+y取得最大值4，则实数a的值为（ ）