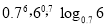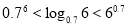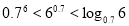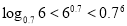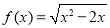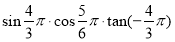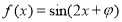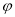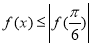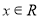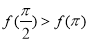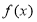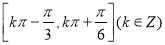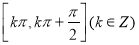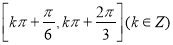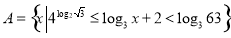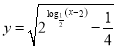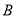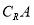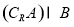题目内容
已知函数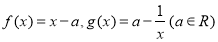 .
.
(1)判断函数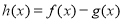 在
在 的单调性并用定义证明;
的单调性并用定义证明;
(2)令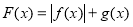 ,求
,求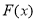 在区间
在区间 的最大值的表达式
的最大值的表达式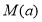 .
.
(1)函数 在
在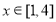 递增;证明详见答案解析.
递增;证明详见答案解析.
(2)当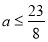 时,
时,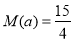 ;当
;当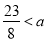 时,
时, .
.
【解析】
试题分析:(1)先根据已知条件求出 ,再根据单调性的定义证明即可;
,再根据单调性的定义证明即可;
(2)由(1)先求出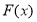 的表达式,再根据单调性求得各个区间的最大值,综上即可求出
的表达式,再根据单调性求得各个区间的最大值,综上即可求出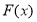 在区间
在区间 的最大值的表达式
的最大值的表达式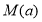 .
.
试题解析:(1) 在
在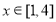 递增;
递增;
证明如下:
在区间 上任取
上任取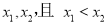
则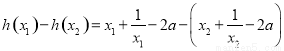
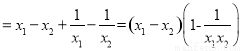
而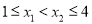 ,所以
,所以 ,
,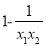 >0
>0
所以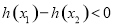 ,即函数
,即函数 在
在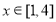 的单调递增;(6分)
的单调递增;(6分)
(2)若 ,
,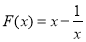 ,在
,在 递增,
递增,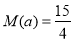 ,
,
若 ,
,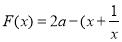 )在
)在 递减,
递减, , (9分)
, (9分)
若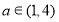 ,则
,则 (11分)
(11分)
当 时,函数递增,
时,函数递增,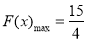 ,
,
当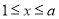 时,函数递减,
时,函数递减,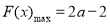 ; (13分)
; (13分)
 ,当
,当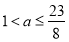 时,
时,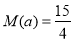 ,当
,当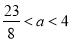 时,
时,
 .
.
综上: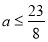 时,
时,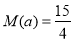 ,当
,当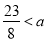 时,
时, . (15分)
. (15分)
考点:函数的单调性、分段函数求值域问题.

练习册系列答案
相关题目