题目内容
如图,直角坐标系xOy所在平面为α,直角坐标系x′Oy′(其中y′与y轴重合)所在的平面为β,∠xOx′=45°.(Ⅰ)已知平面β内有一点P′(2
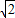 ,2),则点P′在平面α内的射影P的坐标为 ;
,2),则点P′在平面α内的射影P的坐标为 ;(Ⅱ)已知平面β内的曲线C′的方程是(x′-
 )2+2y2-2=0,则曲线C′在平面α内的射影C的方程是 .
)2+2y2-2=0,则曲线C′在平面α内的射影C的方程是 .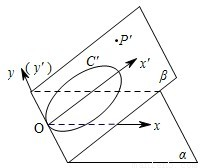
【答案】分析:(I)根据两个坐标系之间的关系,由题意知点P′在平面上的射影P距离x轴的距离不变是2,距离y轴的距离变成2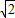 cos45°,写出坐标.
cos45°,写出坐标.
(II)设出所给的图形上的任意一点的坐标,根据两坐标系之间的坐标关系,写出这点的对应的点,根据所设的点满足所给的方程,代入求出方程.
解答:解:(I)由题意知点P′在平面上的射影P距离x轴的距离不变是2,
距离y轴的距离变成2 cos45°=2,
cos45°=2,
∴点P′在平面α内的射影P的坐标为(2,2)
(II)设(x′-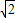 )2+2y2-2=0上的任意点为A(x,y),A在平面α上的射影是(x,y)
)2+2y2-2=0上的任意点为A(x,y),A在平面α上的射影是(x,y)
根据上一问的结果,得到x=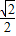 x,y=y,
x,y=y,
∵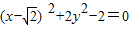 ,
,
∴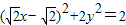
∴(x-1)2+y2=1,
故答案为:(2,2);(x-1)2+y2=1.
点评:本题考查平行投影及平行投影作图法,考查两个坐标系之间的坐标关系,是一个比较简单的题目,认真读题会得分.
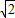 cos45°,写出坐标.
cos45°,写出坐标.(II)设出所给的图形上的任意一点的坐标,根据两坐标系之间的坐标关系,写出这点的对应的点,根据所设的点满足所给的方程,代入求出方程.
解答:解:(I)由题意知点P′在平面上的射影P距离x轴的距离不变是2,
距离y轴的距离变成2
 cos45°=2,
cos45°=2,∴点P′在平面α内的射影P的坐标为(2,2)
(II)设(x′-
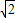 )2+2y2-2=0上的任意点为A(x,y),A在平面α上的射影是(x,y)
)2+2y2-2=0上的任意点为A(x,y),A在平面α上的射影是(x,y)根据上一问的结果,得到x=
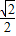 x,y=y,
x,y=y,∵
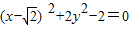 ,
,∴
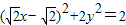
∴(x-1)2+y2=1,
故答案为:(2,2);(x-1)2+y2=1.
点评:本题考查平行投影及平行投影作图法,考查两个坐标系之间的坐标关系,是一个比较简单的题目,认真读题会得分.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
 如图,直角坐标系xOy所在平面为α,直角坐标系x′Oy′(其中y′与y轴重合)所在的平面为β,∠xOx′=45°.
如图,直角坐标系xOy所在平面为α,直角坐标系x′Oy′(其中y′与y轴重合)所在的平面为β,∠xOx′=45°.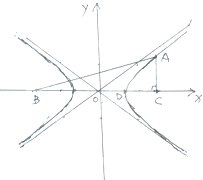 如图,直角坐标系xoy中,有Rt△ABC,∠C=90°,D在边BC上,BD=3DC,双曲线E以B、C为焦点,且经过A、D两点.
如图,直角坐标系xoy中,有Rt△ABC,∠C=90°,D在边BC上,BD=3DC,双曲线E以B、C为焦点,且经过A、D两点. 如图,直角坐标系xOy中,一直角三角形ABC,∠C=90°,B、C在x轴上且关于原点O对称,D在边BC上,BD=3DC,△ABC的周长为12.若一双曲线E以B、C为焦点,且经过A、D两点.
如图,直角坐标系xOy中,一直角三角形ABC,∠C=90°,B、C在x轴上且关于原点O对称,D在边BC上,BD=3DC,△ABC的周长为12.若一双曲线E以B、C为焦点,且经过A、D两点. (2012•蓝山县模拟)如图,直角坐标系xOy中,一直角三角形ABC,∠=90°,B、C在x轴上且关于原点O对称,D在边BC上,BD=3DC,△ABC的周长为12.若一双曲线E以B、C为焦点,且经过A、D两点.
(2012•蓝山县模拟)如图,直角坐标系xOy中,一直角三角形ABC,∠=90°,B、C在x轴上且关于原点O对称,D在边BC上,BD=3DC,△ABC的周长为12.若一双曲线E以B、C为焦点,且经过A、D两点. 如图在直角坐标系xoy中,圆O与x轴交于A、B两点,且|AB|=4,定直线l垂直于x轴正半轴,且到圆心O的距离为4,点P是圆O上异于A、B的任意一点,直线PA、PB分别交l于点M、N.
如图在直角坐标系xoy中,圆O与x轴交于A、B两点,且|AB|=4,定直线l垂直于x轴正半轴,且到圆心O的距离为4,点P是圆O上异于A、B的任意一点,直线PA、PB分别交l于点M、N.