题目内容
函数f(x)=ln
的图象只可能是
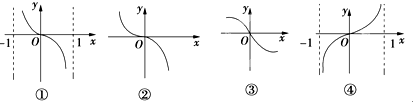
| 1-x | 1+x |
①
①

分析:先求函数的定义域,即可排除②③;再取x=
,又可排除④,从而得出答案.
| 1 |
| 2 |
解答:解:∵
>0,解得-1<x<1,∴函数f(x)=ln
的定义域为{x|-1<x<1}.故可排除②③.
取x=
,则f(
)=ln
<0,故可排除④.
∵
=
-1,当-1<x<1时,可知0<1+x,函数1+x单调递增,∴
-1单调递减,∴函数y=ln
单调递减.因此函数图象只可能是①.
故答案为①.
| 1-x |
| 1+x |
| 1-x |
| 1+x |
取x=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
∵
| 1-x |
| 1+x |
| 2 |
| 1+x |
| 2 |
| 1+x |
| 1-x |
| 1+x |
故答案为①.
点评:取特殊值可排除错误的答案,是解选择题常用方法之一,要注意领会和应用.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目