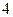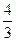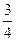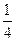题目内容
已知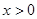 ,
,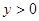 ,
,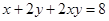 ,则
,则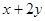 的最小值是( )
的最小值是( )
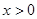 ,
,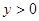 ,
,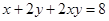 ,则
,则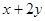 的最小值是( )
的最小值是( )A.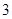 | B.4 | C.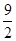 | D.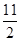 |
B
分析:首先分析题目由已知x>0,y>0,x+2y+2xy=8,求x+2y的最小值,猜想到基本不等式的用法,利用a+b≥2
 代入已知条件,化简为函数求最值.
代入已知条件,化简为函数求最值.解答:解:考察基本不等式x+2y=8-x?(2y)≥8-(
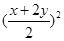 ,
,整理得(x+2y)2+4(x+2y)-32≥0
即(x+2y-4)(x+2y+8)≥0,又x+2y>0,
所以x+2y≥4
故选B.
点评:此题主要考查基本不等式的用法,对于不等式a+b≥2
 在求最大值最小值的问题中应用非常广泛,需要同学们多加注意.
在求最大值最小值的问题中应用非常广泛,需要同学们多加注意.
练习册系列答案
相关题目
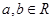 ,且
,且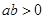 ,则下列不等式中,恒成立的是 ( )
,则下列不等式中,恒成立的是 ( )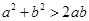
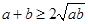
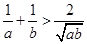
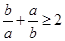
 的解集为( )
的解集为( )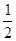 ,1)∪(1,
,1)∪(1, )
) 、
、 都为正数,且
都为正数,且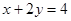 ,则lgx+lgy的最大值是
,则lgx+lgy的最大值是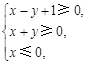 则z=x+2y的最大值是 ▲
则z=x+2y的最大值是 ▲ 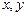 满足
满足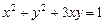 ,则
,则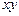 的最大值是_____ ___
的最大值是_____ ___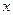 的不等式
的不等式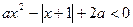 的解集为空集,则实数
的解集为空集,则实数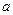 的取值范围为 ▲ .
的取值范围为 ▲ .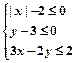 所表示的平面区域为
所表示的平面区域为 ,若
,若 、
、 为
为 |的最大值为
|的最大值为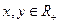 ,且
,且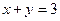 ,则
,则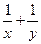 的最小值为 ( )
的最小值为 ( )