Question

（2003•北京）有三个新兴城镇分别位于A、B、C三点处，且AB=AC=a，BC=2b，今计划合建一个中心医院，为同时方便三镇，准备建在BC的垂直平分线上的P点处（建立坐标系如图）．
（Ⅰ）若希望点P到三镇距离的平方和最小，则P应位于何处？
（Ⅱ）若希望点P到三镇的最远距离为最小，则P应位于何处？

Answer 1

分析：（I）设出P的坐标，表示出P至三镇距离的平方和，利用配方法，可得结论；
（II）记h=

a2-b2

，表示出P至三镇的最远距离，分类讨论，确定函数的单调性，从而可得结论．

解答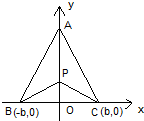：解：（Ⅰ）由题设条件a＞b＞0，设P的坐标为（0，y），则P至三镇距离的平方和为f(y)=2(b2+y2)+(

a2-b2

-y)2=3y2-2

a2-b2

y+a2+b2
所以，当y=

a2-b2

3

时，函数f（y）取得最小值．
答：点P的坐标是(0，

a2-b2

3

)
（Ⅱ）记h=

a2-b2

P至三镇的最远距离为g(x)=

b2+y2 ，当 b2+y2 ≥|h-y| |h-y|，当 b2+y2 ＜|h-y|.

由

b2+y2

≥|h-y|解得y≥

h2-b2

2h

，记y*=

h2-b2

2h

，
于是g(x)=

b2+y2 ，当y≥y* |h-y|，当y＜y*.

当y*=

h2-b2

2h

≥0，即h≥b时，
因为

b2+y2

在[y^*，+∞）上是增函数，而|h-y|在（-∞，y^*]上是减函数．
所以y=y^*时，函数g（y）取得最小值．点P的坐标是(0，

h2-b2

2h

)
当y*=

h2-b2

2h

＜0，即h＜b时，因为

b2+y2

在[y^*，+∞）上当y=0函数g（y）取得最小值b，而|h-y|在（-∞，y^*]上是减函数，且|h-y|＞b，所以y=0时，函数g（y）取得最小值．
答：当h≥b时，点P的坐标是(0，

h2-b2

2h

)；当h＜b时，点P的坐标是（0，0），其中h=

a2-b2

点评：本小题主要考查函数，不等式等基本知识，考查运用数学知识分析问题和解决问题的能力．