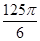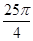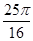题目内容
一个四面体ABCD的所有棱长都为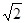 ,四个顶点在同一球面上,则此球的表面积为( )
,四个顶点在同一球面上,则此球的表面积为( )
A.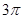 | B.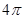 | C.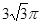 | D. |
A
解析试题分析:如图,将四面体补成正方体,则正方体的棱长是1,正方体的对角线长为: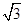 ,则此球的表面积为:
,则此球的表面积为: ,故答案为
,故答案为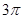 .
.
考点:球的体积和表面积.

练习册系列答案
相关题目
一个几何体的三视图如图所示,则该几何体的表面积是( )
A.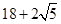 | B.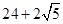 | C. | D.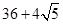 |
已知水平放置的△ABC的直观图△A′B′C′(斜二测画法)是边长为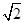 a的正三角形,则原△ABC的面积为( )
a的正三角形,则原△ABC的面积为( )
A.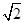 a2 a2 | B.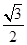 a2 a2 | C.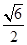 a2 a2 | D. a2 a2 |
在三棱锥A-BCD中,侧棱AB,AC,AD两两垂直,且△ABC,△ACD,△ADB的面积分别为 ,
, ,
, ,则该三棱锥外接球的表面积为( )
,则该三棱锥外接球的表面积为( )
| A.2π | B.6π | C.4 π π | D.24π |
某四棱锥的三视图如图所示,则该四棱锥的体积是( )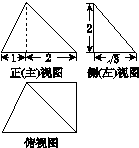
A.5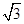 | B.2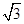 | C.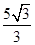 | D.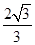 |
某长方体被一个平面所截,得到的几何体的三视图如图所示,则这个几何体的体积为( )
| A.4 | B.4 | C.6 | D.8 |
一个几何体的三视图如图所示,则该几何体的体积为( ).
| A.1 | B. | C. | D. |
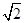 ,AC=2,若四面体ABCD体积的最大值为
,AC=2,若四面体ABCD体积的最大值为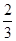 ,则这个球的表面积为( )
,则这个球的表面积为( )