题目内容
已知P为双曲线C: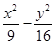 =1上的点,点M满足|
=1上的点,点M满足| 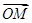 |=1,且
|=1,且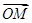 ·
·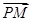 =0,则当|
=0,则当| 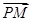 |取得最小值时的点P到双曲线C的渐近线的距离为( )
|取得最小值时的点P到双曲线C的渐近线的距离为( )
A.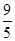 | B.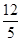 | C.4 | D.5 |
B
解析

练习册系列答案
相关题目
抛物线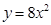 的焦点坐标为( )
的焦点坐标为( )
A. | B.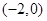 | C. | D. |
设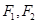 是双曲线
是双曲线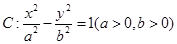 的两个焦点,
的两个焦点, 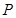 是
是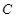 上一点,若
上一点,若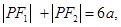 且
且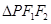 的最小内角为
的最小内角为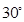 ,则
,则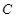 的离心率为( )
的离心率为( )
A.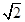 | B.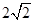 | C.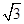 | D.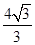 |
已知双曲线C: -
- =1的焦距为10,点P(2,1)在C的渐近线上,则C的方程为( )
=1的焦距为10,点P(2,1)在C的渐近线上,则C的方程为( )
A.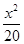 - - =1 =1 | B.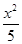 - -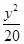 =1 =1 |
C.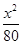 - -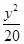 =1 =1 | D.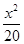 - -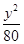 =1 =1 |
在抛物线y=x2+ax-5(a≠0)上取横坐标为x1=-4,x2=2的两点,过这两点引一条割线,有平行于该割线的一条直线同时与抛物线和圆5x2+5y2=36相切,则抛物线顶点的坐标为( )
| A.(-2,-9) | B.(0,-5) |
| C.(2,-9) | D.(1,-6) |
已知抛物线x2=4y上有一条长为6的动弦AB,则AB中点到x轴的最短距离为( )
A. | B. | C.1 | D.2 |
若已知点Q(4,0)和抛物线y= x2+2上一动点P(x,y),则y+|PQ|最小值为( )
x2+2上一动点P(x,y),则y+|PQ|最小值为( )
A.2+2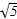 | B.11 | C.1+2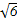 | D.6 |
若抛物线y2=2px(p>0)的焦点在圆x2+y2+2x-3=0上,则p=( )
A. | B.1 | C.2 | D.3 |
已知双曲线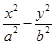 =1(a>0,b>0)的左、右焦点分别为F1,F2,点O为双曲线的中心,点P在双曲线右支上,△PF1F2内切圆的圆心为Q,圆Q与x轴相切于点A,过F2作直线PQ的垂线,垂足为B,则下列结论成立的是( )
=1(a>0,b>0)的左、右焦点分别为F1,F2,点O为双曲线的中心,点P在双曲线右支上,△PF1F2内切圆的圆心为Q,圆Q与x轴相切于点A,过F2作直线PQ的垂线,垂足为B,则下列结论成立的是( )
| A.|OA|>|OB| | B.|OA|<|OB| |
| C.|OA|=|OB| | D.|OA|与|OB|大小关系不确定 |