题目内容
如图,设 点是圆
点是圆 上的动点,过点
上的动点,过点 作圆
作圆 的两条切线,切点分别为
的两条切线,切点分别为 ,切线
,切线 分别交
分别交 轴于
轴于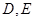 两点.
两点.
(1)求四边形 面积的最小值;
面积的最小值;
(2)是否存在点 ,使得线段
,使得线段 被圆
被圆 在点
在点 处的切线平分?若存在,求出点
处的切线平分?若存在,求出点 的纵坐标;若不存在,说明理由.
的纵坐标;若不存在,说明理由.

【答案】
(1)面积最小值为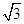
(2)设存在点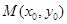 满足条件
满足条件
设过点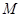 且与圆
且与圆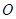 相切的直线方程为:
相切的直线方程为: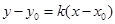
则由题意得,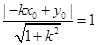 ,化简得:
,化简得: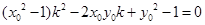
设直线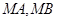 的斜率分别为
的斜率分别为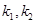 ,则
,则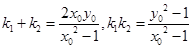
圆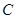 在点
在点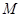 处的切线方程为
处的切线方程为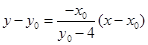
令 ,得切线与
,得切线与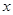 轴的交点坐标为
轴的交点坐标为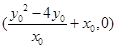
又得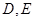 的坐标分别为
的坐标分别为
由题意知,
用韦达定理代入可得,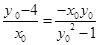 ,与
,与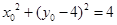 联立,得
联立,得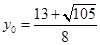
【解析】略

练习册系列答案
相关题目
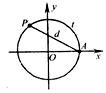 如图,设点
如图,设点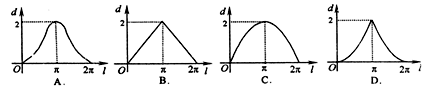
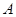 是单位圆上的一定点,动点
是单位圆上的一定点,动点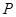 从点
从点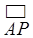 的长为
的长为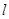 ,弦
,弦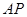 的长为
的长为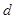 ,则函数
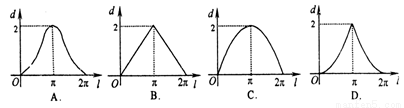
,则函数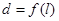 的图像大致是
的图像大致是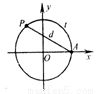
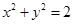 上的动点,点D是P在x轴上的投影。M为线段PD上一点,
上的动点,点D是P在x轴上的投影。M为线段PD上一点,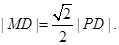
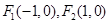 ,设点
,设点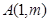
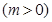 是轨迹C上的一点,求
是轨迹C上的一点,求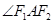 的
的 所在直线的方程。
所在直线的方程。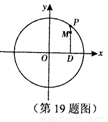
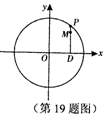 如图,设P是圆
如图,设P是圆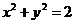 上的动点,点D是P在x轴上的投影。M为线段PD上一点,且
上的动点,点D是P在x轴上的投影。M为线段PD上一点,且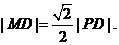
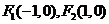 ,设点
,设点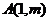
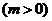 是轨迹C上的一点,求
是轨迹C上的一点,求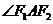 的平分线
的平分线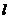 所在直线的方程。
所在直线的方程。