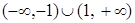题目内容
函数 的递减区间是
的递减区间是
- A.(-3,-1)
- B.(-∞,-1)
- C.(-∞,-3)
- D.(-1,+∞)
A
分析:函数 可由y=
可由y= ,t=(1-x)(x+3)复合而成故函数
,t=(1-x)(x+3)复合而成故函数 的递减区间即是t=(1-x)(x+3)的递增区间和t>0的区间的交集.
的递减区间即是t=(1-x)(x+3)的递增区间和t>0的区间的交集.
解答:∵函数 可由y=
可由y= ,t=(1-x)(x+3)复合而成并且y=
,t=(1-x)(x+3)复合而成并且y= 在t∈(0,+∞)单调递减
在t∈(0,+∞)单调递减
∴函数 的递减区间即为t=(1-x)(x+3)的增区间和(1-x)(x+3)>0的解集的交集
的递减区间即为t=(1-x)(x+3)的增区间和(1-x)(x+3)>0的解集的交集
又∵t=(1-x)(x+3)的增区间为(-∞,-1),(1-x)(x+3)>0的解集为(-3,1)
∴函数 的递减区间为(-3,-1)
的递减区间为(-3,-1)
故选A
点评:此题主要考查了利用复合函数的单调性求单调区间.解题的关键首先将复合函数转化为几个基本函数然后利用复合函数的单调性法则-同增异减来决定求内层函数的增区间还是减区间同时要注意定义域的限制!
分析:函数
 可由y=
可由y= ,t=(1-x)(x+3)复合而成故函数
,t=(1-x)(x+3)复合而成故函数 的递减区间即是t=(1-x)(x+3)的递增区间和t>0的区间的交集.
的递减区间即是t=(1-x)(x+3)的递增区间和t>0的区间的交集.解答:∵函数
 可由y=
可由y= ,t=(1-x)(x+3)复合而成并且y=
,t=(1-x)(x+3)复合而成并且y= 在t∈(0,+∞)单调递减
在t∈(0,+∞)单调递减 ∴函数
 的递减区间即为t=(1-x)(x+3)的增区间和(1-x)(x+3)>0的解集的交集
的递减区间即为t=(1-x)(x+3)的增区间和(1-x)(x+3)>0的解集的交集又∵t=(1-x)(x+3)的增区间为(-∞,-1),(1-x)(x+3)>0的解集为(-3,1)
∴函数
 的递减区间为(-3,-1)
的递减区间为(-3,-1)故选A
点评:此题主要考查了利用复合函数的单调性求单调区间.解题的关键首先将复合函数转化为几个基本函数然后利用复合函数的单调性法则-同增异减来决定求内层函数的增区间还是减区间同时要注意定义域的限制!

练习册系列答案
相关题目
若函数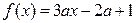 在区间
在区间 上无零点,则函数
上无零点,则函数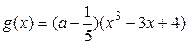 的递减区间是
的递减区间是
A.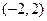 | B.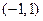 | C.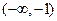 | D. |
 的递减区间是
的递减区间是 或
或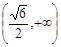 B.
B.
 或
或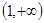 D.
D.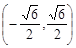
 的递减区间是
的递减区间是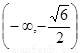 或
或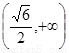 B.
B.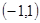
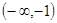 或
或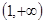 D.
D.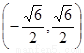
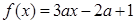 在区间
在区间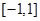 上无零点,则函数
上无零点,则函数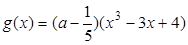 的递减区间是
的递减区间是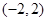 (B)
(B)
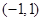 (C)
(C)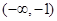 (D)
(D)