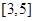题目内容
已知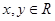 且
且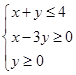 ,则存在
,则存在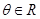 ,使得
,使得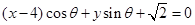 的概率为( )
的概率为( )
A.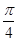 | B.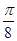 | C.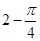 | D. |
D
解析试题分析:可行域是一个三角形,面积为2;又直线系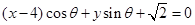 与圆
与圆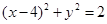 相切,故该三角形不被该直线系扫到的部分是一个半径为
相切,故该三角形不被该直线系扫到的部分是一个半径为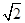 圆心角为
圆心角为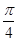 的扇形,面积为
的扇形,面积为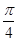 ,从而被直线系扫到部分的面积为
,从而被直线系扫到部分的面积为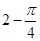 ,故所求概率为
,故所求概率为 .
.
考点:1、不等式组表示的平面区域;2、几何概型.

练习册系列答案
相关题目
当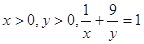 时,
时,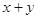 的最小值为( )
的最小值为( )
| A.10 | B.12 | C.14 | D.16 |
设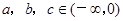 ,则
,则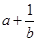 ,
,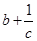 ,
,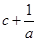 ( )
( )
| A.都不大于-2 | B.都不小于-2 |
| C.至少有一个不小于-2 | D.至少有一个不大于-2 |
若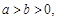 集合
集合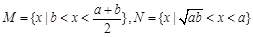 ,则集合
,则集合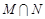 等于( )
等于( )
A.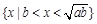 | B.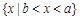 | C.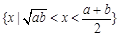 | D.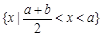 |
已知不等式 的解集为
的解集为 ,点
,点 在直线
在直线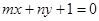 上,其中
上,其中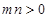 ,则
,则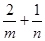 的最小值为( )
的最小值为( )
A.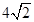 | B.8 | C.9 | D.12 |
若2x+2y=1,则x+y的取值范围是( )
| A.[0,2] | B.[﹣2,0] |
| C.[﹣2,+∞) | D.(﹣∞,﹣2] |
若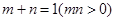 ,则
,则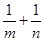 的最小值为( )
的最小值为( )
| A.1 |
| B.2 |
| C.3 |
| D.4 |
若两个正实数x,y满足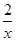 +
+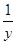 =1,并且x+2y>m2+2m恒成立,则实数m的取值范围是( )
=1,并且x+2y>m2+2m恒成立,则实数m的取值范围是( )
| A.(-∞,-2)∪[4,+∞) | B.(-∞,-4]∪[2,+∞) |
| C.(-2,4) | D.(-4,2) |
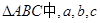 分别是角A、B、C的对边,若
分别是角A、B、C的对边,若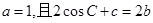 ,则
,则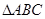 的周长的取值范围是( )
的周长的取值范围是( )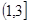 B.
B.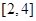 C.
C. D.
D.