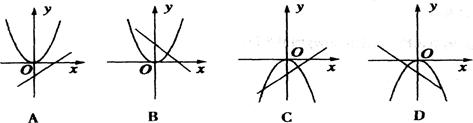
题目内容
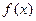是定义在R上的奇函数，下列结论中，不正确的是( )
A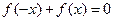． | B． |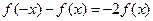
C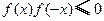． | D． |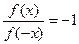
D
解析
练习册系列答案
相关题目
函数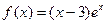
的单调递增区间是
A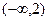． | B．(0,3) | C．(1,4) | D． |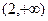
设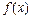
、
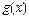分别是定义在
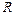上的奇函数和偶函数，当x＜0时，f′(x)g(x)+f(x)g′(x)＞0，且g(-3）=0，则不等式
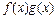＜0的解集是（ ）
| A．｛x｜-3＜x＜0或x＞3｝ | B．｛x｜x＜-3或0＜x＜3｝ |
| C．｛x｜x＜-3或x＞3｝ | D．｛x｜-3＜x＜0或0＜x＜3｝ |
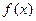是偶函数，且当
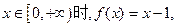则不等式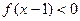
的解集是（ ）
A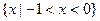． | B． |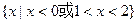
C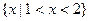． | D． |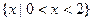
下列函数在区间[0,+∞）上是减函数的为（ ）
A．y=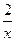 | B．y=1+x2 | C．y=│x-1│ | D．y=1-x2 |
设函数
若
是奇函数，则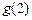
的值是（ ）
A． | B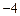． | C．  | D．4 |
下列函数中是奇函数，且在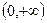
上为增函数的是 （ ）
A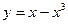． | B． |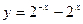
C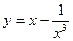． | D． |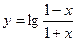
函数
的定义域为
，则函数
的定义域为（ ）
A． | B． | C． | D． |
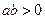时，函数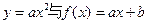
的图象是 ( )