题目内容
某商品一年内出厂价格在6元的基础上按月份随正弦曲线波动,已知3月份达到最高价格8元,7月份价格最低为4元,该商品在商店内的销售价格在8元基础上按月份随正弦曲线波动,5月份销售价格最高为10元,9月份销售价最低为6元,假设商店每月购进这种商品m件,且当月销完,你估计哪个月份盈利最大?
解:设出厂价波动函数为y1=6+Asin(ω1x+φ1)
根据最高价格和最低价格可知A=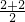 =2 T1=8,ω1=
=2 T1=8,ω1= ,
, +φ1=
+φ1= ,φ1=-
,φ1=-
∴y1=6+2sin( x-
x- )
)
设销售价波动函数为y2=8+Bsin(ω2x+φ2)
易知B=2,T2=8,ω2= ,
, π+φ2=
π+φ2= ,φ2=-
,φ2=-
∴y2=8+2sin( x-
x- )
)
每件盈利 y=y2-y1=[8+2sin( x-
x- )][6+2sin(
)][6+2sin( x-
x- )]=2-2
)]=2-2 sin
sin x
x
当sin x=-1
x=-1  x=2kπ-
x=2kπ- ,x=8k-2时y取最大值
,x=8k-2时y取最大值
当k=1 即x=6时 y最大
∴估计6月份盈利最大
分析:分别设出出厂价波动函数和售价波动函数,利用最高和最低价分别振幅A和B,根据月份求得周期进而求得ω1和ω2,根据最大值求得φ1和φ2,利用y=y2-y1,求得每件盈利的表达式,利用正弦函数的性质求得y取最大值时x的值.
点评:本题主要考查了在实际问题中建立三角函数的模型的问题.突显了运用三角函数的图象和性质来解决问题.
根据最高价格和最低价格可知A=
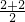 =2 T1=8,ω1=
=2 T1=8,ω1= ,
, +φ1=
+φ1= ,φ1=-
,φ1=-
∴y1=6+2sin(
 x-
x- )
)设销售价波动函数为y2=8+Bsin(ω2x+φ2)
易知B=2,T2=8,ω2=
 ,
, π+φ2=
π+φ2= ,φ2=-
,φ2=-
∴y2=8+2sin(
 x-
x- )
)每件盈利 y=y2-y1=[8+2sin(
 x-
x- )][6+2sin(
)][6+2sin( x-
x- )]=2-2
)]=2-2 sin
sin x
x当sin
 x=-1
x=-1  x=2kπ-
x=2kπ- ,x=8k-2时y取最大值
,x=8k-2时y取最大值当k=1 即x=6时 y最大
∴估计6月份盈利最大
分析:分别设出出厂价波动函数和售价波动函数,利用最高和最低价分别振幅A和B,根据月份求得周期进而求得ω1和ω2,根据最大值求得φ1和φ2,利用y=y2-y1,求得每件盈利的表达式,利用正弦函数的性质求得y取最大值时x的值.
点评:本题主要考查了在实际问题中建立三角函数的模型的问题.突显了运用三角函数的图象和性质来解决问题.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目