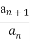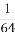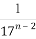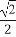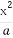Question

已知b>0,直线x-b2y-1=0与直线(b2+1)x+ay+2=0互相垂直,则ab的最小值等于(　　)

(A)1 (B)2 (C)2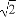 (D)2

 

Answer 1

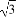
B

【解析】【思路点拨】先由两直线垂直可得到关于a,b的一个等式,再将ab用一个字母来表示,进而求出最值.

∵直线x-b2y-1=0与直线(b2+1)x+ay+2=0互相垂直,

∴(b2+1)-b2a=0,即a=,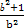

∴a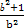b=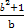()b==b+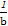≥2(当且仅当b=1时取等号),即ab的最小值等于2.