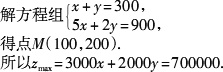题目内容
某公司计划
2009年在甲、乙两个电视台做总时间不超过300分钟的广告，广告总费用不超过9万元，甲、乙电视台的广告收费标准分别为500元/分钟和200元/分钟，规定甲、乙两个电视台为该公司所做的每分钟广告，能给公司带来的收益分别为0.3万元和0.2万元．问该公司应如何分配在甲、乙两个电视台的广告时间，才能使公司的收益最大，最大收益是多少万元？
答案：
解析：
解析：
|
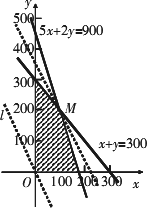
答：该公司在甲电视台做 100分钟广告，在乙电视台做200分钟广告，公司的收益最大，最大收益是70万元．分析：找出线性约束条件和目标函数，从而建立线性规划的数学模型，通过解数学模型得到正确的最优解，回归现实问题并写出答案． 作出二元一次不等式组表示的平面区域，即可行域，如图所示．
目标函数 z＝3000x＋2000y变形为y＝－ x＋ ，得到斜率为－ ，在y轴上的截距为 ，且随z变化的一组平行线．
由图可以看出，当直线 y＝－ x＋ 经过可行域上的点M时，截距最大，即目标函数的取值最大．
点评：本题实质上是以实际问题为载体，利用截距法求最值的线性规划问题．解此类题的关键是能够分析清楚题目给出的相关信息，从中提炼出不等式组，即建模，但在提炼不等式组时，不能有任何遗漏，否则结果将与实际不符合． |
练习册系列答案
相关题目