题目内容
一个正方体,它的表面涂满了红色,把它切割成27个完全相等的小正方体,从中任取2个,其中1个恰有一面涂有红色,另1个恰有两面涂有红色的概率为分析:根据题意,分析可得分割下来的27个小正方体中有一面、二面红色的数目,进而由乘法原理可得从中任取2个,其中1个恰有一面涂有红色,另1个恰有两面涂有红色的情况数目,再结合题意可得从27块中任取两块的情况数目,由古典概型的公式计算可得答案.
解答:解:根据题意,分析可得:
在分割下来的27个完全相等的小正方体中,有6个只有一面有红色,有12个两面有红色,8块有3面红色,而还有一个没有红色;
则从中任取2个,其中1个恰有一面涂有红色,另1个恰有两面涂有红色的情况有12×6种;
而从27块中任取两块,有C27×26种情况;
则从中任取2个,其中1个恰有一面涂有红色,另1个恰有两面涂有红色的概率为
=
;
故答案为:
.
在分割下来的27个完全相等的小正方体中,有6个只有一面有红色,有12个两面有红色,8块有3面红色,而还有一个没有红色;
则从中任取2个,其中1个恰有一面涂有红色,另1个恰有两面涂有红色的情况有12×6种;
而从27块中任取两块,有C27×26种情况;
则从中任取2个,其中1个恰有一面涂有红色,另1个恰有两面涂有红色的概率为
| 12×6 | ||
|
| 8 |
| 39 |
故答案为:
| 8 |
| 39 |
点评:本题考查古典概型的计算,难点在于分析分割下来的27个小正方体中有一面、二面红色以及其他情况的数目,必要时要借助几何体模型或魔方来分析.

练习册系列答案
相关题目
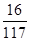 B.
B. C.
C. D.
D.