题目内容
若实数x,y满足x2+y2-2x+4y=0,则x-2y的最大值为
10
10
.分析:先配方为圆的标准方程再画出图形,设z=x-2y,再利用z的几何意义求最值,只需求出直线z=x-2y过图形上的点A的坐标,即可求解.
解答:解:方程x2+y2-2x+4y=0可化为(x-1)2+(y+2)2=5,
即圆心为(1,-2),半径为
的圆,(如图)
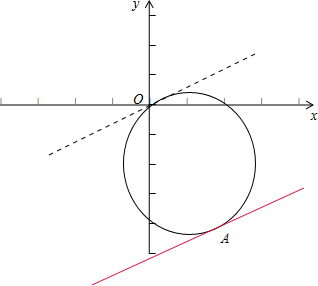
设z=x-2y,将z看做斜率为
的直线z=x-2y在y轴上的截距,
经平移直线知:当直线z=x-2y经过点A(2,-4)时,z最大,
最大值为:10.
故答案为:10.
即圆心为(1,-2),半径为
| 5 |

设z=x-2y,将z看做斜率为
| 1 |
| 2 |
经平移直线知:当直线z=x-2y经过点A(2,-4)时,z最大,
最大值为:10.
故答案为:10.
点评:本题主要考查简单的转化思想和数形结合的思想,利用平移直线法确定位置是解决问题的关键,属中档题..

练习册系列答案
相关题目
若实数x,y满足x2+y2-4x+1=0,则
的最小值是( )
| y |
| x |
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|