题目内容
已知奇函数f(x)的定义域是R,且f(x)=f(1-x),当0≤x≤| 1 | 2 |
(1)求证:f(x)是周期函数;
(2)求f(x)在区间[1,2]上的解析式;
(3)求方程f(x)=log10000x的根的个数.
分析:(1)由于函数为定义在R上的奇函数,根据奇函数的性质可得:f(-x)=-f(x),结合f(x)=f(1-x),我们易得函数
f(x)是周期函数;
(2)由当0≤x≤
时,f(x)=x-x2.根据函数f(x)为奇函数,及f(x)=f(1-x),及(1)中的结论,即可求出求
f(x)在区间[1,2]上的解析式;
(3)根据(1)的结论,根据函数零点的判断方法,结合函数图象即可得到方程f(x)=log10000x的根的个数.
f(x)是周期函数;
(2)由当0≤x≤
| 1 |
| 2 |
f(x)在区间[1,2]上的解析式;
(3)根据(1)的结论,根据函数零点的判断方法,结合函数图象即可得到方程f(x)=log10000x的根的个数.
解答:解:(1)∵函数为定义在R上的奇函数,
∴f(x)=-f(-x),
又∵f(x)=f(1-x),
∴-f(-x)=f(1-x),
即f(x)=-f(x-1),
则f(x-2)=-f[(x-1)-1]=f(x)
故f(x)为周期函数,且T=2
(2)当
≤x≤1时,0≤1-x≤
则f(1-x)=(1-x)-(1-x)2=-x2+x=f(x)
即0≤x≤1时,f(x)=-x2+x
当-1≤x≤0时,0≤-x≤1
则f(-x)=-(-x)2+(-x)=-f(x)
即f(x)=x2+x
当1≤x≤2时,-1≤x-2≤0
f(x-2)=(x-2)2+(x-2)=x2-3x+2=f(x)
即f(x)=x2-3x+2,(1≤x≤2)
(3)由(2)的结论,我们画出函数y=f(x)与y=log10000x的图象如下图所示:
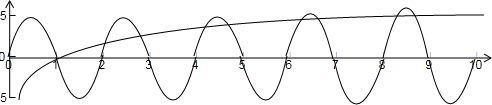
由图可知,两个函数的图象共有9个交点,故方程f(x)=log10000x共有9个根
∴f(x)=-f(-x),
又∵f(x)=f(1-x),
∴-f(-x)=f(1-x),
即f(x)=-f(x-1),
则f(x-2)=-f[(x-1)-1]=f(x)
故f(x)为周期函数,且T=2
(2)当
| 1 |
| 2 |
| 1 |
| 2 |
则f(1-x)=(1-x)-(1-x)2=-x2+x=f(x)
即0≤x≤1时,f(x)=-x2+x
当-1≤x≤0时,0≤-x≤1
则f(-x)=-(-x)2+(-x)=-f(x)
即f(x)=x2+x
当1≤x≤2时,-1≤x-2≤0
f(x-2)=(x-2)2+(x-2)=x2-3x+2=f(x)
即f(x)=x2-3x+2,(1≤x≤2)
(3)由(2)的结论,我们画出函数y=f(x)与y=log10000x的图象如下图所示:

由图可知,两个函数的图象共有9个交点,故方程f(x)=log10000x共有9个根
点评:本题解析的关键点是根据函数的奇偶性,求函数在对称区间上的解析式,若已知函数的奇偶性,及函数在区间[a,b]上的解析式,求对称区间[-b,-a]上的解析式,一般步骤为:取区间上任意一个数,即x∈[-b,-a],则-x∈[a,b],由区间[a,b]上的解析式,写出f(-x)的表达式,根据奇函数f(-x)=-f(x)(偶函数f(-x)=f(x))给出区间[-b,-a]上函数的解析式.

练习册系列答案
相关题目
 已知奇函数f(-x)的定义域为[-1,0)∪(0,1],其图象是两条直线的一部分(如图所示),则不等式f(x)-f(-x)>-1的解集为( )
已知奇函数f(-x)的定义域为[-1,0)∪(0,1],其图象是两条直线的一部分(如图所示),则不等式f(x)-f(-x)>-1的解集为( )