题目内容
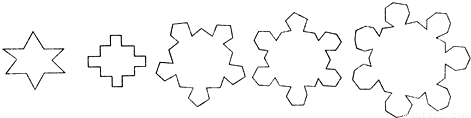
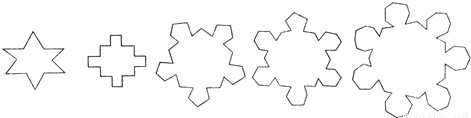
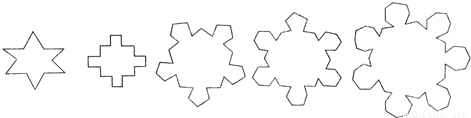
如图,第n(n∈N*)个图形是由正n+2边形“扩展”而来,则第n个图形中共有
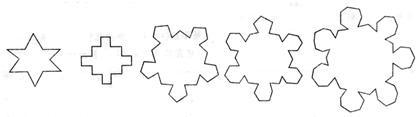
(n+2)(n+3)
(n+2)(n+3)
个顶点(相临两条边的交点即为顶点).
分析:由已知图形中,我们可以列出顶点个数与多边形边数n,然后分析其中的变化规律,然后用归纳推理可以推断出一个一般性的结论.
解答:解:由已知中的图形我们可以得到:
当n=1时,顶点共有12=3×4(个),
n=2时,顶点共有20=4×5(个),
n=3时,顶点共有30=5×6(个),
n=4时,顶点共有42=6×7(个),
…
由此我们可以推断:
第n个图形共有顶点(n+2)(n+3)个,
故答案为:(n+2)(n+3).
当n=1时,顶点共有12=3×4(个),
n=2时,顶点共有20=4×5(个),
n=3时,顶点共有30=5×6(个),
n=4时,顶点共有42=6×7(个),
…
由此我们可以推断:
第n个图形共有顶点(n+2)(n+3)个,
故答案为:(n+2)(n+3).
点评:本题考察的知识点是归纳推理,本类题解答的关键是:先通过观察个别情况发现某些相同性质;然后从已知的相同性质中推出一个明确表达的一般性命题或猜想.

练习册系列答案
 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目