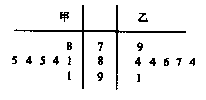题目内容
为迎接2012年伦敦奥运会，在著名的海滨城市青岛举行了一场奥运选拔赛，其中甲、乙两名运动员为争取最后一个参赛名额进行的7轮比赛的得分如茎叶图所示．（1）若从甲运动员的每轮比赛的得分中任选3个不低于80且不高于90的得分，求甲的三个得分与其每轮比赛的平均得分的差的绝对值都不超过2的概率；
（2）若分别从甲、乙两名运动员的每轮比赛不低于80且不高于90的得分中任选1个，求甲、乙两名运动员得分之差的绝对值ξ的分布列与期望．
分析：（1）由茎叶图可得甲运动员七轮比赛的得分情况，计算平均得分，从而可求甲的三个得分与其每轮比赛的平均得分的差的绝对值都不超过2的概率；
（2）确定ξ的可能取值，计算相应的概率，从而可得ξ的分布列与期望．
（2）确定ξ的可能取值，计算相应的概率，从而可得ξ的分布列与期望．
解答：解：（1）由茎叶图可知，甲运动员七轮比赛的得分情况为：78，81，84，85，84，85，91．所以甲每轮比赛的平均得分为
=
=84，
显然甲运动员每轮比赛得分中不低于80且不高于90的得分共有5个，分别为81，84，85，84，85，其中81分与平均得分的绝对值大于2，所求概率P=
=
．
（2）设甲、乙两名运动员的得分分别为x，y，则得分之差的绝对值为ξ=|x-y|．
显然，由茎叶图可知，ξ的可能取值为0，1，2，3，5，6．
当ξ=0时，x=y=84，故P（ξ=0）=
=
当ξ=1时，x=85，y=84或y=86，故P（ξ=1）=
=
当ξ=2时，x=84，y=86或x-85，y=87，故P（ξ=2）=
=
当ξ=3时，x=81，y=84或x=84，y=87，故P（ξ=3）=
=
当ξ=5时，x=81，y=86，故P（ξ=5）=
=
当ξ=6时，x=81，y=87，故P（ξ=6）=
=
所以ξ的分布列为：
Eξ=0×
+1×
+2×
+3×
+5×
+6×
=
．
. |
| x1 |
| 78+81+84+85+84+85+91 |
| 7 |
显然甲运动员每轮比赛得分中不低于80且不高于90的得分共有5个，分别为81，84，85，84，85，其中81分与平均得分的绝对值大于2，所求概率P=
| ||
|
| 2 |
| 5 |
（2）设甲、乙两名运动员的得分分别为x，y，则得分之差的绝对值为ξ=|x-y|．
显然，由茎叶图可知，ξ的可能取值为0，1，2，3，5，6．
当ξ=0时，x=y=84，故P（ξ=0）=
| ||||
|
| 6 |
| 25 |
当ξ=1时，x=85，y=84或y=86，故P（ξ=1）=
| ||||
|
| 8 |
| 25 |
当ξ=2时，x=84，y=86或x-85，y=87，故P（ξ=2）=
| ||||
|
| 4 |
| 25 |
当ξ=3时，x=81，y=84或x=84，y=87，故P（ξ=3）=
| ||||
|
| 1 |
| 5 |
当ξ=5时，x=81，y=86，故P（ξ=5）=
| ||||
|
| 1 |
| 25 |
当ξ=6时，x=81，y=87，故P（ξ=6）=
| ||||
|
| 1 |
| 25 |
所以ξ的分布列为：
| ξ | 0 | 1 | 2 | 3 | 5 | 6 | ||||||||||||
| P |
|
|
|
|
|
|
| 6 |
| 25 |
| 8 |
| 25 |
| 4 |
| 25 |
| 1 |
| 5 |
| 1 |
| 25 |
| 1 |
| 25 |
| 42 |
| 25 |
点评：本题考查概率的计算，考查离散型随机变量的分布列与数学期望，确定的取值，计算概率是关键．
练习册系列答案
相关题目
的分布列与期望。