题目内容
直线y=k(x-a)(a>0)与抛物线y2=2px相交于A、B两点,F(a,0)为焦点,若点P的坐标为(-a,0),则( )A.∠APF<∠BPF
B.∠APF>∠BPF
C.∠APF=∠BPF
D.以上均有可能
【答案】分析:设A(x1,y1),B(x2,y2),不妨设y1>0,y2<0,tan∠APF=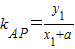 ,tan∠BPF=-
,tan∠BPF=-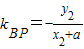 ,联立直线方程与抛物线方程消掉y得x的二次方程,通过作差由韦达定理可得tan∠APF-tan∠BPF=0,从而tan∠APF=tan∠BPF,再由两角的范围可得∠APF=∠BPF.
,联立直线方程与抛物线方程消掉y得x的二次方程,通过作差由韦达定理可得tan∠APF-tan∠BPF=0,从而tan∠APF=tan∠BPF,再由两角的范围可得∠APF=∠BPF.
解答:解:设A(x1,y1),B(x2,y2),不妨设y1>0,y2<0,
由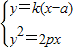 得k2x2-(2ak2+2p)x+k2a2=0(k≠0),
得k2x2-(2ak2+2p)x+k2a2=0(k≠0),
则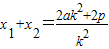 ,
,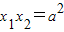 ,
,
tan∠APF=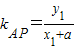 ,tan∠BPF=-
,tan∠BPF=-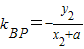 ,
,
因为tan∠APF-tan∠BPF=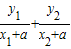 =
=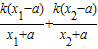
=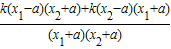
=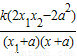 =
=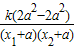 =0,
=0,
所以tan∠APF=tan∠BPF,
又∠APF与∠BPF均为锐角,
所以∠APF=∠BPF,
故选C.
点评:本题考查直线与圆锥曲线的位置关系,考查学生分析解决问题的能力,解决本题的关键是建立两角正切值与直线斜率的关系,通过作差可利用韦达定理解决问题.
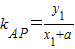 ,tan∠BPF=-
,tan∠BPF=-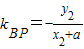 ,联立直线方程与抛物线方程消掉y得x的二次方程,通过作差由韦达定理可得tan∠APF-tan∠BPF=0,从而tan∠APF=tan∠BPF,再由两角的范围可得∠APF=∠BPF.
,联立直线方程与抛物线方程消掉y得x的二次方程,通过作差由韦达定理可得tan∠APF-tan∠BPF=0,从而tan∠APF=tan∠BPF,再由两角的范围可得∠APF=∠BPF.解答:解:设A(x1,y1),B(x2,y2),不妨设y1>0,y2<0,
由
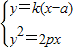 得k2x2-(2ak2+2p)x+k2a2=0(k≠0),
得k2x2-(2ak2+2p)x+k2a2=0(k≠0),则
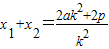 ,
,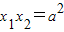 ,
,tan∠APF=
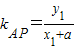 ,tan∠BPF=-
,tan∠BPF=-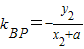 ,
,因为tan∠APF-tan∠BPF=
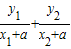 =
=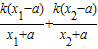
=
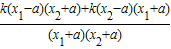
=
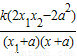 =
=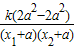 =0,
=0,所以tan∠APF=tan∠BPF,
又∠APF与∠BPF均为锐角,
所以∠APF=∠BPF,
故选C.
点评:本题考查直线与圆锥曲线的位置关系,考查学生分析解决问题的能力,解决本题的关键是建立两角正切值与直线斜率的关系,通过作差可利用韦达定理解决问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 总有公共点,则实数a的取值范围是( )
总有公共点,则实数a的取值范围是( )
