题目内容
若函数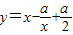
在（1，+∞）上单调递增，则实数a的取值范围是（ ）A．（-∞，-1]
B．[-1，+∞）
C．（-∞，1]
D．[1，+∞）
【答案】分析：先利用导数求函数的单调增区间，求导，令导数大于0，因为函数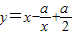
在（1，+∞）上单调递增，所以当
x＞1时，导数横大于等于0，再据此判断参数a的范围．
解答：解：∵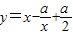
，∴
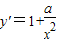
∵函数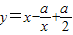
在（1，+∞）上单调递增，
∴当x∈（1，+∞），y′≥0恒成立
即当x∈（1，+∞），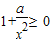
恒成立
∴a≥-1，a的取值范围是[-1，+∞）
故选B
点评：本题主要考查了应用导数求函数的单调区间，属于导数的常规题．
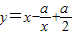在（1，+∞）上单调递增，所以当x＞1时，导数横大于等于0，再据此判断参数a的范围．
解答：解：∵
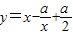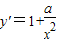
，∴∵函数
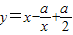在（1，+∞）上单调递增，∴当x∈（1，+∞），y′≥0恒成立
即当x∈（1，+∞），
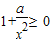恒成立∴a≥-1，a的取值范围是[-1，+∞）
故选B
点评：本题主要考查了应用导数求函数的单调区间，属于导数的常规题．
练习册系列答案
相关题目