题目内容
红队队员甲、乙、丙分别与蓝队队员A、B、C进行围棋比赛,甲对A,乙对B,丙对C各一局,已知甲胜A、乙胜B、丙胜C的概率分别为
,
,
,若各局比赛结果相互独立,用X表示红队队员获胜的总局数,则X的数学期望EX=
| 3 |
| 5 |
| 1 |
| 2 |
| 1 |
| 2 |
1.6
1.6
.分析:由题意知X的可能取值是0,1,2,3,结合变量对应的事件写出变量对应的概率,变量等于2使得概率可以用1减去其他的概率得到,由此能算出期望.
解答:解:由题意知X的可能取值是0,1,2,3.
P(X=0)=0.4×0.5×0.5=0.1.
P(X=1)=0.4×0.5×0.5+0.4×0.5×0.5+0.6×0.5×0.5=0.35.
P(X=3)=0.6×0.5×0.5=0.15.
P(X=2)=1-0.1-0.35-0.15=0.4.
∴EX=0×0.1+1×0.35+2×0.4+3×0.15=1.6.
故答案为:1.6.
P(X=0)=0.4×0.5×0.5=0.1.
P(X=1)=0.4×0.5×0.5+0.4×0.5×0.5+0.6×0.5×0.5=0.35.
P(X=3)=0.6×0.5×0.5=0.15.
P(X=2)=1-0.1-0.35-0.15=0.4.
∴EX=0×0.1+1×0.35+2×0.4+3×0.15=1.6.
故答案为:1.6.
点评:题考查互斥事件的概率,考查相互独立事件的概率,考查离散型随机变量的分布列和期望,解题时注意对立事件概率的使用,一般遇到从正面解决比较麻烦的,就选择利用对立事件来解决.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
 表示红队队员获胜的总盘数,求
表示红队队员获胜的总盘数,求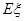 .
.