题目内容
(本小题满分12分)
如图某市现有自市中心O通往正西和北偏东30°方向的两条主要公路,为了解决该市交通拥挤问题,市政府决定修建一条环城公路.分别在通往正西和北偏东30°方向的公路上选用A、B两点,使环城公路在A、B间为直线段,要求AB路段与市中心O的距离为10 km,且使A、B间的距离|AB|最小.请你确定A、B两点的最佳位置.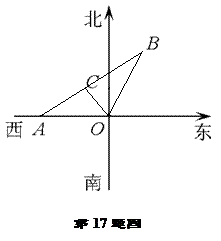
如图,令|OA|=a,|OB|=b,则在△AOB中,∠AOB=120°. …………2分
∴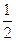 |OC||AB|=
|OC||AB|=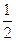 absin120°.
absin120°.
∴|AB|= . ① …………………………………………………………4分
. ① …………………………………………………………4分
又由余弦定理,
|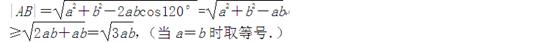 ② …………………6分
② …………………6分
由①②知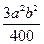 ≥3ab.
≥3ab.
∵ab>0,∴ab≥400 ③ ……………………………………………8分
③代入①得|AB|=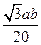 ≥20
≥20 .
.
当a=b时|AB|取得最小值.…………………………………………………10分
而a=b时,△AOB为等腰三角形,
∴∠OAB=∠OBA=30°.
∴a=b=20.
∴A、B两点的最佳位置是距市中心O均为20km处. ………………………12分
解析

练习册系列答案
相关题目
 ,
,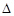 ABC中,已知
ABC中,已知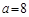 ,
,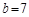 ,
,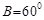 ,求
,求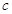 .
.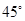 且与点A相距40
且与点A相距40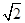 海里的位置B,经过40分钟又测得该船已行驶到点A北偏东
海里的位置B,经过40分钟又测得该船已行驶到点A北偏东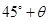 (其中
(其中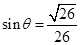 ,
,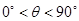 )且与点A相距10
)且与点A相距10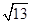 海里的位置C.
海里的位置C. 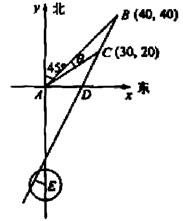
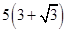 海里的两个观测点,现位于A点北偏东45°,B点北偏西60°的D点有一艘轮船发出求救信号,位于B点南偏西60°且与B点相距
海里的两个观测点,现位于A点北偏东45°,B点北偏西60°的D点有一艘轮船发出求救信号,位于B点南偏西60°且与B点相距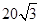 海里的C点的救援船立即即前往营救,其航行速度为30海里/小时,该救援船到达D点需要多长时间?
海里的C点的救援船立即即前往营救,其航行速度为30海里/小时,该救援船到达D点需要多长时间?
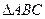 中,角
中,角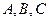 所对的
所对的 边为
边为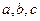 ,已知
,已知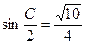 。
。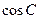 的值;
的值;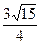 ,且
,且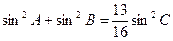 ,求
,求 ,求
,求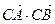 的最大值
的最大值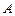 岛,已知
岛,已知 四周
四周 海里内有暗礁,现一货轮由
海里内有暗礁,现一货轮由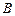 处望见
处望见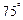 ,再航行
,再航行 海里到
海里到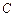 后,见
后,见 ,
,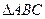 中,
中,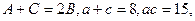 求
求 的值。
的值。