题目内容
已知向量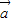 和
和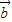 的夹角为120°,且|
的夹角为120°,且|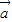 |=2,|
|=2,|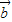 |=5,则(2
|=5,则(2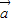 -
-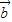 )•
)•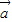 = .
= .?
【答案】分析:由向量数量积的运算性质可得(2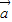 -
-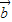 )•
)•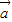 =
=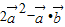 ,代入已知即可求解
,代入已知即可求解
解答:解:∵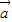 和
和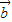 的夹角为120°,且|
的夹角为120°,且|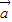 |=2,|
|=2,|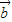 |=5,
|=5,
则(2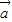 -
-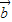 )•
)•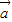 =
=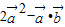 =8-2×5×cos120°=13
=8-2×5×cos120°=13
故答案为:13
点评:本题主要考查了向量的数量积的基本运算性质的应用,解题的关键是 数练应用基本公式.
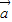 -
-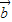 )•
)•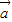 =
=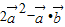 ,代入已知即可求解
,代入已知即可求解解答:解:∵
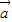 和
和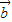 的夹角为120°,且|
的夹角为120°,且|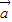 |=2,|
|=2,|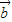 |=5,
|=5,则(2
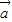 -
-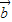 )•
)•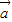 =
=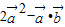 =8-2×5×cos120°=13
=8-2×5×cos120°=13故答案为:13
点评:本题主要考查了向量的数量积的基本运算性质的应用,解题的关键是 数练应用基本公式.

练习册系列答案
相关题目
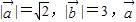 和
和 的夹角为45°,求:
的夹角为45°,求: 与λ
与λ 的夹角为钝角时,λ的取值范围;
的夹角为钝角时,λ的取值范围; 与λ
与λ 的夹角的余弦值.
的夹角的余弦值. 和
和 的夹角为30°,
的夹角为30°,
 (2)求
(2)求 .
.