题目内容
已知函数
时取得最大值，则f（x）在[-π，0]上的单调增区间是（ ）A．
B．
C．
D．
【答案】分析：函数f（x）=Asin（x+φ）（A＞0）在
取最大值可得，
=A⇒sin（
+φ）=1，结合
可求φ，从而可求函数的解析式，再求函数的单调增区间．
解答：解：因为函数f（x）=Asin（x+φ）（A＞0）在
取最大值
所以可得，
=A⇒sin（
+φ）=1
又因为
所以 φ=
而
（A＞0）与y=sin（x-
）的单调性相同且[-π，0]
故函数在[
]上单调递增，在[-π，
]上单调递减
故选D
点评：本题由函数的部分图象的性质求函数的解析式，由函数的解析式进一步求函数的单调区间，熟练掌握函数的性质并能灵活应用是解决本题的关键．
取最大值可得，=A⇒sin（+φ）=1，结合 可求φ，从而可求函数的解析式，再求函数的单调增区间．解答：解：因为函数f（x）=Asin（x+φ）（A＞0）在
取最大值所以可得，
=A⇒sin（+φ）=1又因为
所以 φ=而
（A＞0）与y=sin（x-）的单调性相同且[-π，0]故函数在[
]上单调递增，在[-π，]上单调递减故选D
点评：本题由函数的部分图象的性质求函数的解析式，由函数的解析式进一步求函数的单调区间，熟练掌握函数的性质并能灵活应用是解决本题的关键．
练习册系列答案
相关题目
时取得最大值，则f(x)在
上的单调增区间是
时取得最大值，则f(x)在[－π，0]上的单调增区间是
时取得最大值，则f（x）在[-π，0]上的单调增区间是（ ）
时取得最大值4.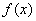
的最小正周期；
.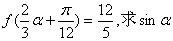