题目内容
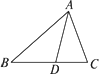
如图所示，已知△ADB和△ADC都是以D为直角顶点的直角三角形，且AD=BD=CD，∠BAC=60°．求证：BD⊥平面ADC．分析：不妨设AD=BD=CD=1，则由题意可得AB=AC=
，AD⊥BD．根据
•
=（
-
）•
=
•
-
•
，计算
•
=1，
•
=1，
可得
•
=0，即BD⊥AC．再利用直线和平面垂直的判定定理证得BD⊥平面ADC．
| 2 |
| BD |
| AC |
| AD |
| AB |
| AC |
| AD |
| AC |
| AB |
| AC |
| AD |
| AC |
| AB |
| AC |
可得
| BD |
| AC |
解答：证明：不妨设AD=BD=CD=1，则由题意可得AB=AC=
，AD⊥BD，AD⊥DC．故有
•
=0．
∵
•
=（
-
）•
=
•
-
•
，
由于
•
=
•（
+
）=
•
=1，
•
=|
|•|
|cos 60°=
×
×
=1．
∴
•
=0，即BD⊥AC．
又已知AD∩AC=A，∴BD⊥平面ADC．
| 2 |
| AD |
| DC |
∵
| BD |
| AC |
| AD |
| AB |
| AC |
| AD |
| AC |
| AB |
| AC |
由于
| AD |
| AC |
| AD |
| AD |
| DC |
| AD |
| AD |
| AB |
| AC |
| AB |
| AC |
| 2 |
| 2 |
| 1 |
| 2 |
∴
| BD |
| AC |
又已知AD∩AC=A，∴BD⊥平面ADC．
点评：本题主要考查证明直线和平面垂直的方法，两个向量数量积的运算，属于中档题．
练习册系列答案
相关题目
，
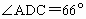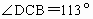，问收到命令时飞机应该沿什么航向飞行，此时离城市C的距离是多少？
，
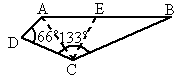
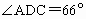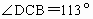，问收到命令时飞机应该沿什么航向飞行，此时离城市C的距离是多少？
．
、
是△
的高，且AB∶AD＝
∶
，∠C＝∠
．
＝
·BE．