题目内容
有下列命题:(1)若sinα>0,则α为锐角或钝角;
(2)若sinα>sinβ,则α>β;
(3)y=tanα的定义域为{α|α≠
| π |
| 2 |
(4)sin(
| 7 |
| 2 |
其中正确的命题是
分析:令 α=-330°,可得 (1)不正确; 令α=-300°,β=30°,可得(2)不正确;要使y=tanα有意义,角的终边不能在y轴上,故α≠kπ+
,k∈z,故(3)正确;根据正弦函数的周期性及诱导公式可得(4)正确.
| π |
| 2 |
解答:解:(1)不正确,如 α=-330°时,sinα>0,但 α并不是锐角或钝角.
(2)不正确,如 α=-300°,β=30° 时,sinα=
,sinβ=
,显然α>β 不成立.
(3)不正确,要使y=tanα有意义,角的终边不能在y轴上,故α≠kπ+
,k∈z,
∴y=tanα的定义域为 {α|α≠
+kπ,k∈Z}.
(4)正确,根据正弦函数的周期性及诱导公式可得 sin(
-α )=sin(
-α)=-cosα.
故答案为 (4).
(2)不正确,如 α=-300°,β=30° 时,sinα=
| ||
| 2 |
| 1 |
| 2 |
(3)不正确,要使y=tanα有意义,角的终边不能在y轴上,故α≠kπ+
| π |
| 2 |
∴y=tanα的定义域为 {α|α≠
| π |
| 2 |
(4)正确,根据正弦函数的周期性及诱导公式可得 sin(
| 7π |
| 2 |
| 3π |
| 2 |
故答案为 (4).
点评:通过给变量取特殊值,举反例来说明某个命题不正确,是一种简单有效的方法.

练习册系列答案
相关题目
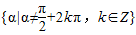 ;
; ;
;