题目内容
设实数a=(| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 5 |
分析:根据指数函数与对数函数的单调性,只要比较a,b,c与0、1的大小即可得到答案.
解答:解:由对数函数f(x)=log
x是减函数可得:b=log
3<log
1=0,所以b=log
3<0,
由指数函数f(x)=(
)x是减函数可得:a=(
)0.2<(
)0=1,所以0<a=(
)0.2<1,
由指数函数f(x)=2x是增函数可得:c=2
>20=1,所以c=2
>1.
故答案为b<a<c.
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 5 |
由指数函数f(x)=(
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 5 |
由指数函数f(x)=2x是增函数可得:c=2
| 1 |
| 5 |
| 1 |
| 5 |
故答案为b<a<c.
点评:解决此类问题的关键是熟练掌握指数函数与对数函数的单调性,并且熟练利用函数的单调性比较函数值的大小.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
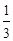 x3-
x3-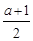 x2+ax.
x2+ax. .
.