题目内容
(本小题满分12分)
设关于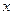 的方程
的方程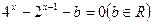
(Ⅰ)若方程有实数解,求实数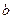 的取值范围;
的取值范围;
(Ⅱ)当方程有实数解时,讨论方程实根的个 数,并求出方程的解.
数,并求出方程的解.
设关于
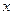 的方程
的方程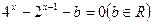
(Ⅰ)若方程有实数解,求实数
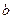 的取值范围;
的取值范围;(Ⅱ)当方程有实数解时,讨论方程实根的个
 数,并求出方程的解.
数,并求出方程的解.解:(Ⅰ)原方程为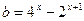 ,
,
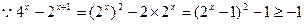 ,
,
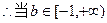 时方程有实数解;-------------------------4分
时方程有实数解;-------------------------4分
(Ⅱ)①当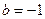 时,
时,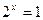 ,∴方程有唯一解
,∴方程有唯一解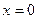 ;
; ----6分
----6分
②当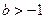 时,
时,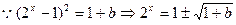 .
.
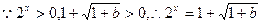 的解为
的解为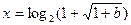 ;--8分
;--8分
令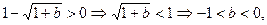
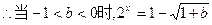 的解为
的解为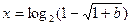 ;--10分
;--10分
综合①、②,得
1)当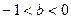 时原方程有两解:
时原方程有两解: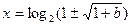 ;
;
2)当 时,原方程有唯一解
时,原方程有唯一解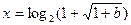 ;-------12分
;-------12分
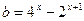 ,
,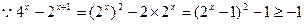 ,
,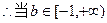 时方程有实数解;-------------------------4分
时方程有实数解;-------------------------4分(Ⅱ)①当
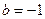 时,
时,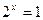 ,∴方程有唯一解
,∴方程有唯一解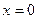 ;
; ----6分
----6分②当
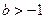 时,
时,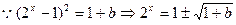 .
.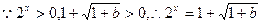 的解为
的解为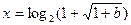 ;--8分
;--8分令
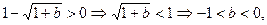
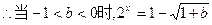 的解为
的解为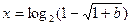 ;--10分
;--10分综合①、②,得
1)当
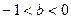 时原方程有两解:
时原方程有两解: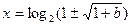 ;
;2)当
 时,原方程有唯一解
时,原方程有唯一解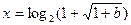 ;-------12分
;-------12分略

练习册系列答案
相关题目


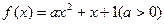 的两个不同的零点为
的两个不同的零点为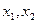
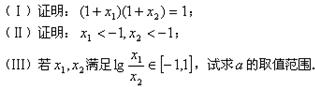
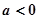 ,则函数
,则函数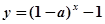 的图象必过点 ( )
的图象必过点 ( )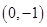
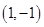
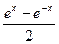 的反函数( )。
的反函数( )。 是定义在R上的奇函数,当
是定义在R上的奇函数,当 =
= 。
。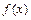 是定义在
是定义在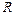 上的奇函数,当
上的奇函数,当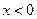 时,
时,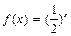 ,那么
,那么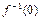 的值为( )
的值为( )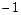

 ,
, 则
则 的取值范围是 ______
的取值范围是 ______