题目内容
某汽车公司有两家装配厂，生产甲、乙两种不同型号的汽车，若A厂每小时可完成1辆甲型车和2辆乙型车；B厂每小时可完成3辆甲型车和1辆乙型车．今欲制造40辆甲型车和20辆乙型车，问这两家工厂各工作几小时，才能使所费的总工作时数最少？分析：利用线性规划的思想方法解决某些实际问题属于直线方程的一个应用．本题主要考查找出约束条件与目标函数，准确地描画可行域，再利用图形直线求得满足题设的最优解．
解答：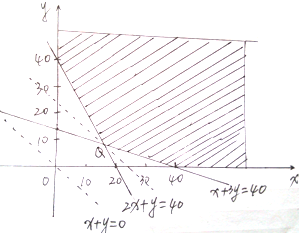
解：设A厂工作xh，B厂工作yh，总工作时数为th，则t=x+y，
且x+3y≥40，2x+y≥20，x≥0，y≥0，
可行解区域如图．
而符合问题的解为此区域内的格子点（纵、横坐标都是整数的点称为格子点），
于是问题变为要在此可行解区域内，
找出格子点（x，y），使t=x+y的值为最小．
由图知当直线l：y=-x+t过Q点时，
纵、横截距t最小，但由于符合题意的解必须是格子点，
我们还必须看Q点是否是格子点．
解方程组
得Q（4，12）为格子点．
故A厂工作4h，B厂工作12h，可使所费的总工作时数最少．
解：设A厂工作xh，B厂工作yh，总工作时数为th，则t=x+y，且x+3y≥40，2x+y≥20，x≥0，y≥0，
可行解区域如图．
而符合问题的解为此区域内的格子点（纵、横坐标都是整数的点称为格子点），
于是问题变为要在此可行解区域内，
找出格子点（x，y），使t=x+y的值为最小．
由图知当直线l：y=-x+t过Q点时，
纵、横截距t最小，但由于符合题意的解必须是格子点，
我们还必须看Q点是否是格子点．
解方程组
|
得Q（4，12）为格子点．
故A厂工作4h，B厂工作12h，可使所费的总工作时数最少．
点评：用图解法解决线性规划问题时，分析题目的已知条件，找出约束条件和目标函数是关键，可先将题目中的量分类、列出表格，理清头绪，然后列出不等式组（方程组）寻求约束条件，并就题目所述找出目标函数．然后将可行域各角点的值一一代入，最后比较，即可得到目标函数的最优解．
练习册系列答案
相关题目