题目内容
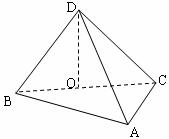
如下图,把边长为1的正方形![]() 沿对角线
沿对角线![]() 折起得到三棱锥
折起得到三棱锥![]() ,
,![]() 是
是![]() 边上一点.
边上一点.
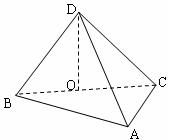
(Ⅰ)求![]() 的取值范围;
的取值范围;
(Ⅱ)当![]() 取最小值时,证明:
取最小值时,证明:![]() 平面
平面![]() ;
;
(Ⅲ)若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
解:(Ⅰ)设在∆DBC中,边BC上的高为h,则![]()
又依题意可求得![]()
∴![]()
(Ⅱ)若DO取最小值,则DO⊥BC
∵![]()
∴O为BC中点,故AO⊥BC
又![]() ,∴
,∴![]() 平面
平面![]()
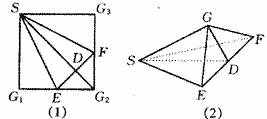
(Ⅲ)解法1:作AE⊥DC,垂足为E,设O为BC中点,连结OE
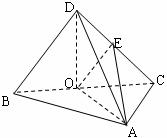
∵![]() ,∴△DAC是等边三角形
,∴△DAC是等边三角形
∴E为DC中点,∴OE∥DB
∴OE⊥DC,∴∠AEO为所求二面角的平面角
∵![]()
∴![]() ,∴AO⊥OE
,∴AO⊥OE
∴![]()
解法2:∵![]() ,
,![]() ,
,![]()
![]() 两两垂直
两两垂直
以O为原点,![]() 分别为
分别为![]() 轴的正方向建立空间直角坐标系,
轴的正方向建立空间直角坐标系,
则各点坐标如下:![]() ,
,
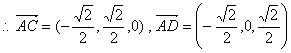 ,
,
设平面ACD的一个法向量为![]() ,则
,则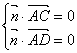 即
即 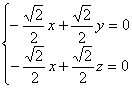
令![]() 得到
得到![]() 又因为
又因为![]() 平面BCD,所以平面BCD的一个法向量为
平面BCD,所以平面BCD的一个法向量为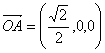 ,
,
设二面角![]() 的平面角为
的平面角为![]() ,则
,则

练习册系列答案
相关题目
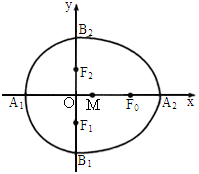
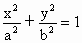 (x≥0)与半椭圆
(x≥0)与半椭圆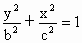 (x≤0)合成的曲线称作“果圆”,其中
(x≤0)合成的曲线称作“果圆”,其中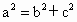 ,a>0,b>c>0.如下图,点
,a>0,b>c>0.如下图,点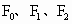 是相应椭圆的焦点,
是相应椭圆的焦点,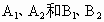 分别是“果圆”与x、y轴的交点.
分别是“果圆”与x、y轴的交点.
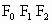 是边长为1的等边三角形,求“果圆”的方程;
是边长为1的等边三角形,求“果圆”的方程;
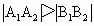 时,求
时,求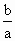 的取值范围;
的取值范围;