题目内容
若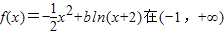 上是减函数,则b的取值范围是( )
上是减函数,则b的取值范围是( )A.[-1,+∞)
B.(-1,+∞)
C.(-∞,-1]
D.(-∞,-1)
【答案】分析:先对函数进行求导,根据导函数小于0时原函数单调递减即可得到答案.
解答:解:由题意可知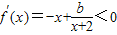 ,在x∈(-1,+∞)上恒成立,
,在x∈(-1,+∞)上恒成立,
即b<x(x+2)在x∈(-1,+∞)上恒成立,
由于y=x(x+2)在(-1,+∞)上是增函数且y(-1)=-1,所以b≤-1,
故选C
点评:本题主要考查导数的正负和原函数的增减性的问题.即导数大于0时原函数单调递增,当导数小于0时原函数单调递减.
解答:解:由题意可知
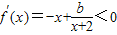 ,在x∈(-1,+∞)上恒成立,
,在x∈(-1,+∞)上恒成立,即b<x(x+2)在x∈(-1,+∞)上恒成立,
由于y=x(x+2)在(-1,+∞)上是增函数且y(-1)=-1,所以b≤-1,
故选C
点评:本题主要考查导数的正负和原函数的增减性的问题.即导数大于0时原函数单调递增,当导数小于0时原函数单调递减.

练习册系列答案
相关题目
 上是减函数,则b的取值范围是( )
上是减函数,则b的取值范围是( ) 上是减函数,则b的取值范围是( )
上是减函数,则b的取值范围是( ) 上是减函数,则b的取值范围是( )
上是减函数,则b的取值范围是( ) 上是减函数,则b的取值范围是( )
上是减函数,则b的取值范围是( )