题目内容
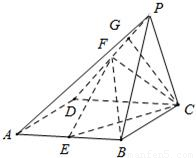
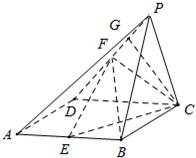 如图,已知面PBC⊥矩形ABCD所在平面,△PBC是边长为2的等边三角形,四边形ABCD是正方形,且E、F分别为AB、PD的中点;
如图,已知面PBC⊥矩形ABCD所在平面,△PBC是边长为2的等边三角形,四边形ABCD是正方形,且E、F分别为AB、PD的中点;(1)求证:EF∥平面PBC;
(2)点G在PD上移动,求证:EF⊥CG;
(3)求三棱锥C-BEF的体积.
分析:(1)取PC的中点H,连接FH,EF,BH,根据三角形的中位线定理,及矩形的性质,可得四边形EBHF为平行四边形,即EF∥BH,再由线面平行的判定定理,即可得到答案.
(2)由已知中面PBC⊥矩形ABCD所在平面,△PBC是边长为2的等边三角形,四边形ABCD是正方形,由等边三角形三线合一的性质可得BH⊥PC,由正方形的性质及面面垂直的性质可得DC⊥BH,由线面垂直的判定定理可得BH⊥平面PCD,结合(1)中结论及线面垂直的第二判定定理可得EF⊥平面PCD,再由线面垂直的性质得到EF⊥CG;
(3)由E、F分别为AB、PD的中点,我们可以分析出三棱锥C-BEF与棱锥P-ABCD高及底面面积的关系,求出棱锥P-ABCD的体积后,即可得到三棱锥C-BEF的体积.
(2)由已知中面PBC⊥矩形ABCD所在平面,△PBC是边长为2的等边三角形,四边形ABCD是正方形,由等边三角形三线合一的性质可得BH⊥PC,由正方形的性质及面面垂直的性质可得DC⊥BH,由线面垂直的判定定理可得BH⊥平面PCD,结合(1)中结论及线面垂直的第二判定定理可得EF⊥平面PCD,再由线面垂直的性质得到EF⊥CG;
(3)由E、F分别为AB、PD的中点,我们可以分析出三棱锥C-BEF与棱锥P-ABCD高及底面面积的关系,求出棱锥P-ABCD的体积后,即可得到三棱锥C-BEF的体积.
解答:证明:(1)取PC的中点H,连接FH,EF,BH
∵E、F分别为AB、PD的中点
 ∴FH∥CD且FH=
∴FH∥CD且FH=
CD,
又由ABCD为矩形
∴FH∥AB且FH=
AB,
即四边形EBHF为平行四边形
即EF∥BH
又∵EF?平面PBC,BH?平面PBC
∴EF∥平面PBC;
(2)∵△PBC是边长为2的等边三角形,
∴BH⊥PC,
又∵四边形EBHF为平行四边形
∴DC⊥BC
又由面PBC⊥矩形ABCD所在平面,
∴DC⊥面PBC
又∵BH?面PBC
∴DC⊥BH
又由PC∩BH=H
∴BH⊥平面PCD
由(1)得EF∥BH
∴EF⊥平面PCD
由CG?平面PCD
∴EF⊥CG;
(3)过P点作PI⊥BC,易得PI即为棱锥P-ABCD的高,且PI=
则VP-ABCD=
•2•2•
=
又∵E、F分别为AB、PD的中点;
∴三棱锥C-BEF的高是棱锥P-ABCD的高的一半,
三棱锥C-BEF的底面面积是棱锥P-ABCD的底面面积的四分之一,
∴VC-BEF=
∵E、F分别为AB、PD的中点
 ∴FH∥CD且FH=
∴FH∥CD且FH=| 1 |
| 2 |
又由ABCD为矩形
∴FH∥AB且FH=
| 1 |
| 2 |
即四边形EBHF为平行四边形
即EF∥BH
又∵EF?平面PBC,BH?平面PBC
∴EF∥平面PBC;
(2)∵△PBC是边长为2的等边三角形,
∴BH⊥PC,
又∵四边形EBHF为平行四边形
∴DC⊥BC
又由面PBC⊥矩形ABCD所在平面,
∴DC⊥面PBC
又∵BH?面PBC
∴DC⊥BH
又由PC∩BH=H
∴BH⊥平面PCD
由(1)得EF∥BH
∴EF⊥平面PCD
由CG?平面PCD
∴EF⊥CG;
(3)过P点作PI⊥BC,易得PI即为棱锥P-ABCD的高,且PI=
| 3 |
则VP-ABCD=
| 1 |
| 3 |
| 3 |
4
| ||
| 3 |
又∵E、F分别为AB、PD的中点;
∴三棱锥C-BEF的高是棱锥P-ABCD的高的一半,
三棱锥C-BEF的底面面积是棱锥P-ABCD的底面面积的四分之一,
∴VC-BEF=
| ||
| 6 |
点评:本题考查的知识点是直线与平面平行的判定,直线与平面垂直的判定与性质,棱锥的体积,其中根据已知条件,添加适当的辅助线,选择恰当的判定方法,是解答此类问题的关键.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
 如图,已知四棱锥P--ABC的底面ABCD为正方形,PA⊥平面ABCD,PA=AB=2,e为PC的中点,F为AD的中点.
如图,已知四棱锥P--ABC的底面ABCD为正方形,PA⊥平面ABCD,PA=AB=2,e为PC的中点,F为AD的中点.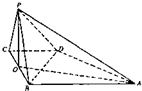 19、如图,已知四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,AB=BC=2CD=2,PB=PC,侧面PBC⊥底面ABCD,O是BC的中点.
19、如图,已知四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,AB=BC=2CD=2,PB=PC,侧面PBC⊥底面ABCD,O是BC的中点.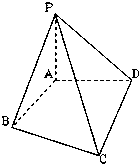 如图,已知PA⊥面ABCD,PA=AB=AD=
如图,已知PA⊥面ABCD,PA=AB=AD=