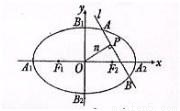
题目内容
如图,椭圆C2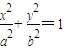 的焦点为F1,F2,|A1B1|=
的焦点为F1,F2,|A1B1|=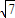 ,S□B1A1B2A2=2S□B1F1B2F2.
,S□B1A1B2A2=2S□B1F1B2F2.(Ⅰ)求椭圆C的方程;
(Ⅱ)设n为过原点的直线,l是与n垂直相交与点P,与椭圆相交于A,B两点的直线|
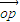 |=1,是否存在上述直线l使
|=1,是否存在上述直线l使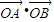 =0成立?若存在,求出直线l的方程;并说出;若不存在,请说明理由.
=0成立?若存在,求出直线l的方程;并说出;若不存在,请说明理由.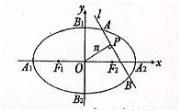
【答案】分析:(Ⅰ)由题意可知a2+b2=7,a=2c,由此能够求出椭圆C的方程.
(Ⅱ)设A、B两点的坐标分别为A(x1,y1),B(x2,y2),假设使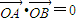 成立的直线l存在.
成立的直线l存在.
(i)当l不垂直于x轴时,根据题设条件能够推出直线l不存在.
(ii)当l垂直于x轴时,满足|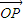 |=1的直线l的方程为x=1或x=-1,由A、B两点的坐标为
|=1的直线l的方程为x=1或x=-1,由A、B两点的坐标为 或
或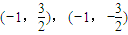 .当x=1时,
.当x=1时,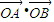 =-
=-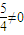 .当x=-1时,
.当x=-1时,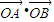 =-
=-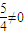 .所以此时直线l也不存在.由此可知,使
.所以此时直线l也不存在.由此可知,使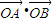 =0成立的直线l不成立.
=0成立的直线l不成立.
解答: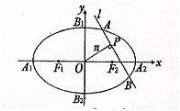 解:(Ⅰ)由题意可知a2+b2=7,
解:(Ⅰ)由题意可知a2+b2=7,
∵S□B1A1B2A2=2S□B1F1B2F2,
∴a=2c.
解得a2=4,b2=3,c2=1.
∴椭圆C的方程为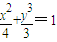 .
.
(Ⅱ)设A、B两点的坐标分别为A(x1,y1),B(x2,y2),假设使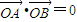 成立的直线l存在.
成立的直线l存在.
(i)当l不垂直于x轴时,设l的方程为y=kx+m,由l与n垂直相交于P点,且|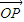 |=1得
|=1得
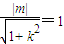 ,即m2=k2+1,由
,即m2=k2+1,由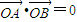 得x1x2+y1y2=0,将y=kx+m代入椭圆得(3+4k2)x2+8kmx+(4m2-12)=0,
得x1x2+y1y2=0,将y=kx+m代入椭圆得(3+4k2)x2+8kmx+(4m2-12)=0,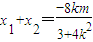 ,①,
,①,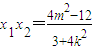 ,②
,②
0=x1x2+y1y2=x1x2+(kx1+m)(kx2+m)=x1x2+k2x1x2+km(x1+x2)+m2
把①②代入上式并化简得(1+k2)(4m2-12)-8k2m2+m2(3+4k2)=0,③
将m2=1+k2代入③并化简得-5(k2+1)=0矛盾.即此时直线l不存在.
(ii)当l垂直于x轴时,满足|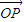 |=1的直线l的方程为x=1或x=-1,
|=1的直线l的方程为x=1或x=-1,
由A、B两点的坐标为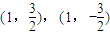 或
或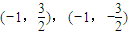 .
.
当x=1时,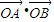 =
=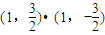 =-
=-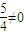 .
.
当x=-1时,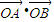 =
=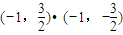 =-
=-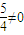 .
.
∴此时直线l也不存在.
综上所述,使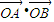 =0成立的直线l不成立.
=0成立的直线l不成立.
点评:本题综合考查直线和椭圆的位置关系,解题时要认真审题,灵活地运用公式.
(Ⅱ)设A、B两点的坐标分别为A(x1,y1),B(x2,y2),假设使
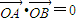 成立的直线l存在.
成立的直线l存在.(i)当l不垂直于x轴时,根据题设条件能够推出直线l不存在.
(ii)当l垂直于x轴时,满足|
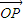 |=1的直线l的方程为x=1或x=-1,由A、B两点的坐标为
|=1的直线l的方程为x=1或x=-1,由A、B两点的坐标为 或
或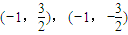 .当x=1时,
.当x=1时,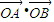 =-
=-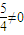 .当x=-1时,
.当x=-1时,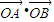 =-
=-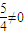 .所以此时直线l也不存在.由此可知,使
.所以此时直线l也不存在.由此可知,使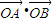 =0成立的直线l不成立.
=0成立的直线l不成立.解答:
 解:(Ⅰ)由题意可知a2+b2=7,
解:(Ⅰ)由题意可知a2+b2=7,∵S□B1A1B2A2=2S□B1F1B2F2,
∴a=2c.
解得a2=4,b2=3,c2=1.
∴椭圆C的方程为
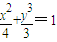 .
.(Ⅱ)设A、B两点的坐标分别为A(x1,y1),B(x2,y2),假设使
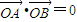 成立的直线l存在.
成立的直线l存在.(i)当l不垂直于x轴时,设l的方程为y=kx+m,由l与n垂直相交于P点,且|
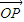 |=1得
|=1得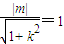 ,即m2=k2+1,由
,即m2=k2+1,由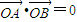 得x1x2+y1y2=0,将y=kx+m代入椭圆得(3+4k2)x2+8kmx+(4m2-12)=0,
得x1x2+y1y2=0,将y=kx+m代入椭圆得(3+4k2)x2+8kmx+(4m2-12)=0,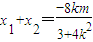 ,①,
,①,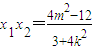 ,②
,②0=x1x2+y1y2=x1x2+(kx1+m)(kx2+m)=x1x2+k2x1x2+km(x1+x2)+m2
把①②代入上式并化简得(1+k2)(4m2-12)-8k2m2+m2(3+4k2)=0,③
将m2=1+k2代入③并化简得-5(k2+1)=0矛盾.即此时直线l不存在.
(ii)当l垂直于x轴时,满足|
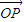 |=1的直线l的方程为x=1或x=-1,
|=1的直线l的方程为x=1或x=-1,由A、B两点的坐标为
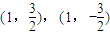 或
或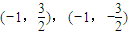 .
.当x=1时,
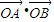 =
=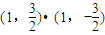 =-
=-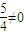 .
.当x=-1时,
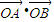 =
=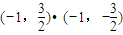 =-
=-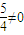 .
.∴此时直线l也不存在.
综上所述,使
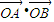 =0成立的直线l不成立.
=0成立的直线l不成立.点评:本题综合考查直线和椭圆的位置关系,解题时要认真审题,灵活地运用公式.

练习册系列答案
相关题目
 焦点在
焦点在 轴上,左、右顶点分别为A1、A,上顶点为B.抛物线C1、C:分别以A、B为焦点,其顶点均为坐标原点O,C1与C2相交于直线
轴上,左、右顶点分别为A1、A,上顶点为B.抛物线C1、C:分别以A、B为焦点,其顶点均为坐标原点O,C1与C2相交于直线 上一点P.
上一点P.
 与直线OP垂直,且与椭圆C交于不同两点M、N,已知点Q(
与直线OP垂直,且与椭圆C交于不同两点M、N,已知点Q( ,0),求
,0),求 的最小值.
的最小值.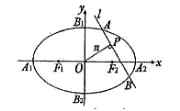 如图,椭圆C2
如图,椭圆C2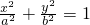 的焦点为F1,F2,|A1B1|=
的焦点为F1,F2,|A1B1|= ,S□B1A1B2A2=2S□B1F1B2F2.
,S□B1A1B2A2=2S□B1F1B2F2.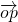 |=1,是否存在上述直线l使
|=1,是否存在上述直线l使 =0成立?若存在,求出直线l的方程;并说出;若不存在,请说明理由.
=0成立?若存在,求出直线l的方程;并说出;若不存在,请说明理由.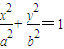 的焦点为F1,F2,|A1B1|=
的焦点为F1,F2,|A1B1|=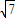 ,S□B1A1B2A2=2S□B1F1B2F2.
,S□B1A1B2A2=2S□B1F1B2F2.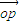 |=1,是否存在上述直线l使
|=1,是否存在上述直线l使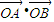 =0成立?若存在,求出直线l的方程;并说出;若不存在,请说明理由.
=0成立?若存在,求出直线l的方程;并说出;若不存在,请说明理由.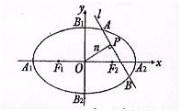
 的焦点为F1,F2,|A1B1|=
的焦点为F1,F2,|A1B1|=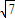 ,S□B1A1B2A2=2S□B1F1B2F2.
,S□B1A1B2A2=2S□B1F1B2F2.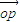 |=1,是否存在上述直线l使
|=1,是否存在上述直线l使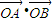 =0成立?若存在,求出直线l的方程;并说出;若不存在,请说明理由.
=0成立?若存在,求出直线l的方程;并说出;若不存在,请说明理由.