题目内容
在平面内,已知双曲线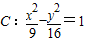 的焦点为F1,F2,则|PF1|-|PF2|=6是点P在双曲线C上的( )
的焦点为F1,F2,则|PF1|-|PF2|=6是点P在双曲线C上的( )A.充要条件
B.充分不必要条件
C.必要不充分条件
D.既不充分又不必要条件
【答案】分析:双曲线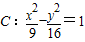 的焦点为F1,F2,由|PF1|-|PF2|=6,知点P在双曲线C上;由点P在双曲线C上,知|PF1|-|PF2|=6,或|PF1|-|PF2|=-6.
的焦点为F1,F2,由|PF1|-|PF2|=6,知点P在双曲线C上;由点P在双曲线C上,知|PF1|-|PF2|=6,或|PF1|-|PF2|=-6.
解答:解:∵双曲线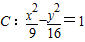 的焦点为F1,F2,
的焦点为F1,F2,
∴|PF1|-|PF2|=6⇒点P在双曲线C上,
点P在双曲线C上⇒|PF1|-|PF2|=6,或|PF1|-|PF2|=-6.
所以|PF1|-|PF2|=6是点P在双曲线C上的充分不必要条件.
故选B.
点评:本题考查必要条件、充分条件与充分要条件的判断,解题时要认真双曲线的定义和性质的合理运用.
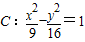 的焦点为F1,F2,由|PF1|-|PF2|=6,知点P在双曲线C上;由点P在双曲线C上,知|PF1|-|PF2|=6,或|PF1|-|PF2|=-6.
的焦点为F1,F2,由|PF1|-|PF2|=6,知点P在双曲线C上;由点P在双曲线C上,知|PF1|-|PF2|=6,或|PF1|-|PF2|=-6.解答:解:∵双曲线
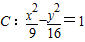 的焦点为F1,F2,
的焦点为F1,F2,∴|PF1|-|PF2|=6⇒点P在双曲线C上,
点P在双曲线C上⇒|PF1|-|PF2|=6,或|PF1|-|PF2|=-6.
所以|PF1|-|PF2|=6是点P在双曲线C上的充分不必要条件.
故选B.
点评:本题考查必要条件、充分条件与充分要条件的判断,解题时要认真双曲线的定义和性质的合理运用.

练习册系列答案
相关题目
 的焦
的焦 ,则
,则 是点
是点 在双曲线
在双曲线 上的
( )
上的
( )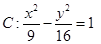 的焦点为
的焦点为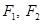 ,则
,则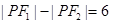 是点
是点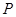 在双曲线
在双曲线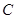 上的
( )
上的
( )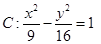 的焦点为
的焦点为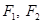 ,则
,则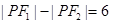 是点
是点 在双曲线
在双曲线 上的(
)
上的(
)