题目内容
函数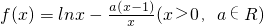 .
.
(1)试求f(x)的单调区间;
(2)当a>0时,求证:函数f(x)的图象存在唯一零点的充要条件是a=1;
(3)求证:不等式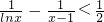 对于x∈(1,2)恒成立.
对于x∈(1,2)恒成立.
解:(1)函数的定义域是(0,+∞),导数f′(x)= -
- ,
,
若a≤0,导数f′(x)在(0,+∞)上大于0,函数的单调增区间是(0,+∞);
若a>0,在(a,+∞)上,导数大于0,函数的单调增区间是(a,+∞),
在(a,+∞)上,导数小于0,单调减区间是(0,a)
(2)由第一问知道,当a>0时候,函数f(x)在(0,a)上递减,在(a,+∞)上递增,
所以要使得函数f(x)的图象存在唯一零点,当且仅当f(a)=0,即a=1
(3)要证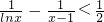 ,即证
,即证 ,即证
,即证
设 恒成立
恒成立
∴g(x)min>g(1)=0,∴g(x)>0,即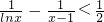
分析:(1)函数的定义域是(0,+∞),求出导数,分a≤0和a>0两种情况讨论导数的符号,得到单调区间.
(2)由函数的单调性知,函数f(x)的图象存在唯一零点,当且仅当f(a)=0.
(3)将要证的不等式等价转化为g(x)>0在区间(1,2)上恒成立,利用导数求出g(x)的最小值,
只要最小值大于0即可.
点评:本题考查利用导数求函数的单调区间即单调性,函数的零点及函数恒成立问题,要证g(x)>0,只要证g(x)
的最小值大于0.
 -
- ,
,若a≤0,导数f′(x)在(0,+∞)上大于0,函数的单调增区间是(0,+∞);
若a>0,在(a,+∞)上,导数大于0,函数的单调增区间是(a,+∞),
在(a,+∞)上,导数小于0,单调减区间是(0,a)
(2)由第一问知道,当a>0时候,函数f(x)在(0,a)上递减,在(a,+∞)上递增,
所以要使得函数f(x)的图象存在唯一零点,当且仅当f(a)=0,即a=1
(3)要证
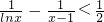 ,即证
,即证 ,即证
,即证
设
 恒成立
恒成立∴g(x)min>g(1)=0,∴g(x)>0,即
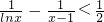
分析:(1)函数的定义域是(0,+∞),求出导数,分a≤0和a>0两种情况讨论导数的符号,得到单调区间.
(2)由函数的单调性知,函数f(x)的图象存在唯一零点,当且仅当f(a)=0.
(3)将要证的不等式等价转化为g(x)>0在区间(1,2)上恒成立,利用导数求出g(x)的最小值,
只要最小值大于0即可.
点评:本题考查利用导数求函数的单调区间即单调性,函数的零点及函数恒成立问题,要证g(x)>0,只要证g(x)
的最小值大于0.

练习册系列答案
相关题目
 .
. 对于x∈(1,2)恒成立.
对于x∈(1,2)恒成立. .
. 对于x∈(1,2)恒成立.
对于x∈(1,2)恒成立. .
. 对于x∈(1,2)恒成立.
对于x∈(1,2)恒成立.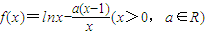 .
. 对于x∈(1,2)恒成立.
对于x∈(1,2)恒成立.